Основні теоретичні відомості. Сила гравітаційного притягання між тілами, маса яких m1і m2, що знаходяться на відстані r:

Сила гравітаційного притягання між тілами, маса яких m₁і m₂, що знаходяться на відстані r:

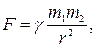
де g = 6,67·10^-11 м³/кг·с² – гравітаційна стала.

Прискорення вільного падіння на полюсі Землі

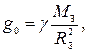
а на відстані r від центру Землі

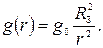
Перша космічна швидкість біля поверхні планети

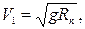
де g – прискорення вільного падіння на поверхні планети;

R_n – радіус планети.

Робота, спрямована на переміщення тіла масою m в гравітаційному полі Землі

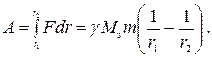
Друга космічна швидкість

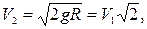
де g – прискорення вільного падіння на поверхні планети;

R_n – радіус планети;

V₁ – перша космічна швидкість.

207. Визначити прискорення вільного падіння g на поверхні Землі за такими заданими величинами: середній радіус Землі R » 6370 км; середня густина Землі r = 5,4 г/см³; гравітаційна стала G = 6,67·10^‑11 Н·м²/кг².

208. Визначити прискорення вільного падіння g на висоті 20 км над поверхнею Землі, приймаючи прискорення вільного падіння на поверхні Землі g₀ = 9,81 м/с², а радіус Землі R » 6370 км.

209. Як зміниться хід маятникового годинника на Місяці порівняно з його ходом на Землі?

210. Визначити мінімальний період обертання супутника нейтронної зірки, якщо густина речовини зірки r = 10¹⁷ кг/м³.

211. Період обертання супутника, що рухається біля поверхні планети, дорівнює Т. Приймаючи планету однорідною кулею, визначити її густину.

212. Радіус земної орбіти – r, радіус Сонця – R. Визначити середню густину речовини Сонця.

213. Визначити густину речовини планети, тривалість доби на якій становить 24 год, якщо на її екваторі тіла невагомі.

214. Знайти відношення сили тяжіння, яка діє на тіло масою m на екваторі та полюсі планети, радіус якої R, маса М і тривалість доби Т.

215. Припустимо, що від поверхні Землі до її центру прорито вузьку шахту і деяке тіло падає з безмежності в цю шахту, досягаючи центру Землі. Яку швидкість буде мати тіло, досягнувши дна шахти, якщо Землю вважати однорідною кулею?

216. З якою швидкістю впаде на поверхню Землі метеорит, швидкість якого вдалині від Землі дуже мала. Опором повітря знехтувати.

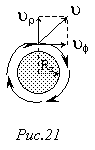
217. Супутник, обертаючись по коловій орбіті радіусом R = 3/2 R_з (R_з – радіус Землі), отримує радіальний імпульс, який надає йому додаткову швидкість u_r, напрямлену від центру Землі по радіусу (рис.21). Яким повинне бути мінімальне значення додаткової швидкості, щоб супутник зміг покинути область земного притягання?

218. Визначити другу космічну швидкість, або швидкість, яку потрібно надати тілу на поверхні Землі для того, щоб воно віддалилось на безмежно велику відстань від Землі. Яким повинен бути напрямок цієї швидкості відносно вертикалі?

219. Знайти відношення сили гравітаційного притягання між двома електронами (і двома протонами) до сили їх електростатичного відштовхування.

220. Знайти потенціальну енергію та силу гравітаційного притягання між однорідною порожнистою сферою масою M і матеріальною точкою масою m.

221. Визначити відношення маси Марса до маси Землі за параметрами орбіти автоматичної станції "Марс-2": максимальне віддалення від поверхні (в апогеї) а = 25000 км, мінімальне (у перигеї) р = 1380 км, період обертання Т = 18 год. Радіус Марса R_м = 3400 км, радіус Землі R » 6400 км.

222. На яку максимальну відстань від Сонця віддаляється комета Галлея? Період обертання її навколо Сонця Т = 76 років, мінімальна відстань, на якій вона проходить від Сонця, R_min = 0,9·10⁸ км. Середній радіус орбіти Землі R₀ = 1,5·10⁸ км.

223. Супутник, запущений на колову орбіту з висотою Н = 500 км над поверхнею Землі, гальмується у верхніх шарах атмосфери. Кутове прискорення супутника b = – 3·10^‑13 рад/с². На якій висоті перебуватиме супутник через місяць? Радіус Землі R_з » 6400 км.

§ 9. Коливання і хвилі.