Основні теоретичні відомості. Рівняння гармонічного коливного руху має такий вигляд:

Рівняння гармонічного коливного руху має такий вигляд:

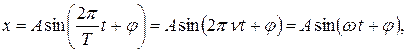
де x – зміщення від положення рівноваги;

A – амплітуда;

T – період;

j – початкова фаза;

n = 1/T – частота коливань,

w = 2p /T – кутова (колова) частота.

Швидкість і прискорення точки, що здійснює коливання, визначається співвідношеннями

224. Побудувати графіки залежності від часу зміщення, швидкості і прискорення при гармонічному коливанні. Побудувати графіки залежності швидкості і прискорення від зміщення. Визначити співвідношення між амплітудами зміщення, швидкості і прискорення.

225. Знайти вираз для потенціальної, кінетичної і повної енергії матеріальної точки масою m, яка здійснює гармонічні коливання за законом x = A·cos wt.

226. Рівняння руху точки задано у вигляді x = sin (p/6)t. Визначити моменти часу, при яких досягаються максимальна швидкість і максимальне прискорення.

227. Записати рівняння гармонічного коливального руху, якщо максимальне прискорення точки 0,493 м/с², період коливань 2 с і зміщення точки від положення рівноваги у початковий момент часу становить 25 мм.

228. Повна енергія тіла, яке здійснює гармонічні коливання, становить 3·10^‑5 Дж, максимальна сила, що діє на тіло дорівнює 1,5·10^-3 Н. Записати рівняння руху цього тіла, якщо період коливань 2 с і початкова фаза 60⁰.

229. Кульку, підвішену на нитці довжиною 2 м, відхиляють на кут 4⁰ і спостерігають її коливання. Вважаючи коливання незагасаючими гармонічними, визначити швидкість кульки у момент проходження нею положення рівноваги. Перевірити одержаний розв'язок, знайшовши швидкість кульки у момент проходження положення рівноваги за законом збереження енергії.

230. До пружини підвішено вантаж масою 10 кг. Знаючи, що пружина під впливом сили 9,8 Н розтягується на 1,5 см, визначити період вертикальних коливань вантажу.

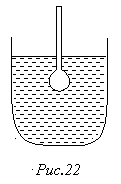
231. Ареометр з циліндричною трубкою діаметром D (рис.22), який плаває у рідині густиною r, отримує невеликий вертикальний поштовх. Визначити період коливань ареометра Т, якщо маса його m – відома. Рух рідини тіл і опір руху ареометра не враховувати.

232. На ракеті, яка злітає вертикально вгору з прискоренням а, вмонтовано маятниковий годинник. Який проміжок часу Т₁ виміряє годинник з моменту старту ракети до падіння її на Землю, якщо двигун працював час Т під час підйому ракети, виміряний за годинником на Землі?

233. Горизонтальна мембрана здійснює синусоїдальні коливання з циклічною частотою w та амплітудою А. На мембрані розміщений маленький тягарець. За якої умови він буде коливатись разом з мембраною і за якої він почне підскакувати?

234. Матеріальна точка під дією квазипружної сили F = -kx здійснює коливання вздовж осі X навколо положення рівноваги. Довести, що середнє за часом значення кінетичної і потенціальної енергії у випадку таких коливаннях однакові.

235. Кулька масою m підвішена на двох послідовно з'єднаних пружинках з коефіцієнтом жорсткості k₁ і k₂. Визначити період вертикальних коливань кульки.

236. 1) визначити амплітуду і початкову фазу гармонічного коливання, одержаного внаслідок додавання однаково напрямлених коливань, заданих рівняннями x₁ = 4 sin pt см і x₂ = 3 sin (pt + p/2) см. 2) записати рівняння результуючого коливання. 3) нарисувати векторну діаграму додавання амплітуд.

237. Записати рівняння результуючого коливання, одержаного внаслідок додаванні двох взаємно перпендикулярних коливань з однаковою частотою n₁ = n₂ = 5 Гц і з однаковою початковою фазою j₁ = j₂ = 60⁰. Амплітуда одного з коливань А₁ = 0,10 м, амплітуда другого А₂ = 0,05 м.

238. Точка бере участь у двох коливаннях однакового періоду з однаковими початковими фазами. Амплітуда коливань А₁ = 3 см і А₂ = 4 см. Визначити амплітуду результуючого коливання, якщо: 1) коливання відбувається в одному напрямку, 2) коливання взаємно перпендикулярні.

239. Точка бере участь одночасно у двох взаємно перпендикулярних коливаннях x = 2 sin wt м і у = 2 cos wt м. Визначити траєкторію руху точки.

240. Точка бере участь одночасно у двох взаємно перпендикулярних коливаннях x = cos pt і у = cos pt/2. Визначити траєкторію результуючого руху точки.

241. Період загасаючих коливань – 4 с, логарифмічний декремент загасання – 1,6, а початкова фаза дорівнює нулю. Зміщення точки при t = T/4 становить 4,5 см. 1) записати рівняння руху цього коливання. 2) побудувати графік цього коливального руху в межах двох періодів.

242. Побудувати графік загасаючого коливання, рівняння якого задається у вигляді 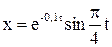м.

243. Рівняння загасаючих коливань задане у вигляді 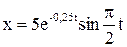м. Визначити швидкість коливної точки в моменти часу: 0, Т, 2Т, 3Т і 4Т.

244. Система здійснює вимушені коливання під дією зовнішньої сили, яка змінюється за гармонічним законом. Довести, що при резонансі за інших однакових умов робота зовнішньої сили за період буде максимальною.

245. Звукові коливання з частотою n = 500 Гц та амплітудою А = 0,25 мм поширюються у повітрі. Довжина хвилі l = 70 см. Визначити: 1) швидкість поширення коливань; 2) максимальну швидкість частинок повітря.

246. Рівняння незагасаючих коливань задається виразом x = 4 sin 600pt см. Визначити зміщення відносно положення рівноваги точки, розташованої на відстані 75 см від джерела коливань, через 0,01 с після початку коливань 300 м/с.

247. Рівняння незагасаючих коливань задається виразом x = sin 2,5pt см. Визначити зміщення відносно положення рівноваги, швидкість і прискорення точки, розташованої на відстані 20 м від джерела коливань, для моменту t = 1 c після початку коливань. Швидкість поширення коливань – 100 м/с.

248. Визначити різницю фаз коливань двох точок, розташованих на відстані відповідно 10 і 16 м від джерела коливань. Період коливань –0,04 с і швидкість поширення – 300 м/с.

249. Зміщення від положення рівноваги точки, розташованої на відстані 4 см від джерела коливань, у момент t = Т/6 дорівнює половині амплітуди. Знайти довжину біжучої хвилі.

250. Визначити довжину хвилі, якщо відстань між першою і четвертою пучностями стоячої хвилі дорівнює 15 см.

§ 10. Механіка рідин і газів.

251. Яка підіймальна сила F 1 м³ гелію, який використовують для наповнення повітряних куль, якщо густина гелію відносно повітря становить 0,137 і 1 м³ повітря важить 12,75 Н?

252. Визначити силу тиску F води на квадратну стінку акваріума (сторона дорівнює а). На якій висоті h від дна перебуває точка прикладання рівнодіючої сил тиску на стінку?

253. На якій висоті h густина повітря у земній атмосфері зменшується вдвічі (передбачається, що температура атмосфери незмінна по всій висоті)? Біля поверхні Землі вважати, що тиск p₀ = 101325 Па і густина повітря r₀ = 1,293 кг/м³.

254. Яка швидкість u витікання рідини з отвору в стінці посудини, якщо висота h рівня рідини над отвором 4,9 м? В'язкість рідини не враховувати.

255. У дні циліндричної посудини є круглий отвір з діаметром d = 1 см. Діаметр посудини D = 0,5 м. Визначити залежність швидкості u пониження рівня води в посудині від висоти h цього рівня, а також числове значення цієї швидкості для висоти h = 0,2 м.

256. У посудину ллється вода, причому за 1 с наливається 0,2 л води. Яким повинен бути діаметр d отвору у дні посудини, щоб вода в ній перебувала на постійному рівні h = 8,3 см?

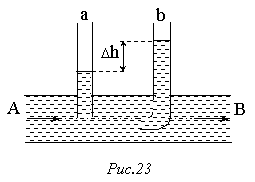
257. По горизонтальній трубі АВ (рис.23) тече рідина. Різниця рівнів цієї рідини у трубках а і b становить 10 см. Діаметри трубок а і b однакові. Визначити швидкість течії рідини у трубі АВ.

258. Якої найбільшої швидкості може досягнути дощова крапля діаметром d = 0,3 мм, якщо коефіцієнт в'язкості повітря h = 1,2·10^-4 Па·с?

259. Стальна кулька діаметром 1 мм падає зі сталою швидкістю 0,185 см/с у великій посудині, наповненій трансформаторним маслом. Визначити коефіцієнт в'язкості трансформаторного масла.

260. Стальна кулька падає у широкій посудині, наповненій трансформаторним маслом, густина якого r = 900 кг/м³, а коефіцієнт в'язкості h = 0,8 Па·с. Вважаючи, що закон Стокса справедливий при Re £ 0,5 (якщо, визначаючи Re за величину D взяти діаметр кульки), обчислити граничне значення діаметра кульки.