Динаміка прямолінійного руху.
83. 1) T = 4,9 Н; 2) Т = 14,7 Н; 3) Т = 8,82 Н.
84. ¦ = 1,63 Н; ¦1 = 3,27 Н.
85. F1 = – (4/5) F.
86. u0 = 2s/t = 10 м/с; F = 2ms/t2 = 2,04 кН.
87. F = kP + 2Ps/gt2.
88. m = 4,9 кг.
89. а = mg/(M + m); T = Mmg/(M + m).
90. a = Mg/(M + m1 + m2 + m3); T1 = (m1 + m2 + m3)a; T2 = (m2 + m3)a; T3 = m3a.
91. a = g (sin a – k cos a).
92. F ³ 39,2 Н.
93. F > (m1 + m2)g.
94. |¦| = |F2|; |F1| = |¦¢|; 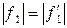 .
.
95. ¦ = M(0,2g + a) + ma = 1146,6 Н.
96. F = 0,25 (M + m)g + 0,5(M + m)g = 22,05 Н.
97. DM = 2(M – P/g)
98. 1) a = 0, T = mg;
2) 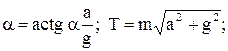
3) a = – j ; T = mg cos j ;
4) tg a = (b/g) cos j / (1 + (b/g) sin j); 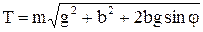 ;
;
5) tg a = – (b/g) cos j / (1 – (b/g) sin j); 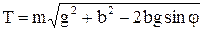 ;
;
99. 1) F = P (k cos a + sin a) = 1,37 кН;
2) F = P (k cos a – sin a) = 590 Н.
100. 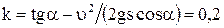 .
.
101. k = 0,5.
102. 1) прискорення всюди дорівнює g. 2) Прискорення каменя максимальне на початку руху і в найнижчій точці його траєкторії.
103. a = g(m1 – m2)/(m1 + m2) = 3,27 м/с2; T1 = T2 = 2m1m2g/(m1+ m2) = 13 Н.
104. a = (m1 sin a – m2)g /(m1 + m2); T = m1m2g(1 + sin a)/(m1 + m2).
105. a = (m1sin b – m2sin a)g /(m1 + m2) = 1,02 м/с2;
T1 = T2 = m1m2g(sin a + sin b)/(m1 + m2) = 5,9 Н.
106. a = g (M(m1 + m2) – 4m1m2 sin a)/(M(m1 + m2) + 4m1m2).
107. m1/m2 = (n + 1)/(n – 1).
108. t » 4,5 с; u » 0,44 м/с.
109. a1 = (2M1 – M2) g /(2M1 + M2/2); a2 = – a1/2; T = 3gM1M2/(4M1 + M2).
110. a1 = g(m1(m2 + m3) – 4m2m3)/m1(m2 + m3) + 4m2m3);
T1 = 8m1m2m3g /(4m2m3 + m1(m2 + m3)); T2 = 4m1m2m3g /(4m2m3 + m1(m2 + m3)).
111. Швидкість більшої кульки буде в 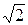 раза більшою ніж швидкість меншої.
раза більшою ніж швидкість меншої.
112. u = 2(r2 – r1)gr2/(9h) = 0,25 см/с.
113. 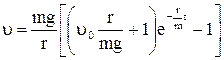
114. 1) 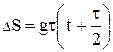 ; 2)
; 2) 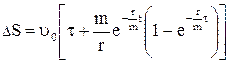 .
.
115. u = mu0 /(m + ru0t).
116. u = u0 exp(– rt /m).
117. 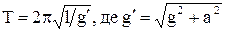 .
.
118. 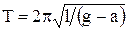 .
.
Дата добавления: 2015-07-24; просмотров: 862;
