Основні теоретичні відомості. Рівняння динаміки для обертального руху тіла відносно осі обертання Oz:

Рівняння динаміки для обертального руху тіла відносно осі обертання Oz:

dL_z/dt = M_z ,

де L_z – проекція вектора моменту імпульсу системи;

M_z – проекція вектора сумарного моменту всіх діючих сил на вісь обертання.

Момент інерції відносно осі обертання Oz:

для матеріальної точки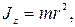

для системи матеріальних точок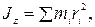

для твердого тіла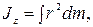

де r – відстань матеріальної точки або елементарної маси dm від осі обертання.

При обертальному твердого тіла навколо осі Oz

L_z = J_zw ,

де w – вектор кутової швидкості тіла.

Теорема Гюйгенса-Штейнера:

J_z = J_Oz+ ma²,

де J_Oz – момент інерції тіла відносно осі обертання, яка проходить через його центр мас;

J_z – момент інерції тіла відносно довільної паралельної осі обертання;

a – відстань між осями.

Моменти інерції тіл правильної геометричної форми відносно головних осей симетрії:

тонкостінний циліндр радіусом R і масою m – J = mR²;

суцільний циліндр радіусом R і масою m – J = mR²/2;

суцільна куля радіусом R і масою m – J = (2/5)mR²;

тонкий однорідний стрижень довжиною l і масою m – J = ml²/12,

(відносно осі, яка проходить через центр мас і перпендикулярна до l).

170. До краю однорідного диска радіусом R = 0,2 м прикладена постійна дотична сила F = 98,1 Н. У процесі обертання на диск діє момент сил тертя М_тр = 4,9 H·м. Визначити масу m диска, коли відомо, що диск обертається з постійним кутовим прискоренням e = 100 рад/с².

171. Маховик, момент інерції якого I = 63,6 кг·м², обертається зі сталою кутовою швидкістю w = 31,4 рад/с. Визначити гальмівний момент М, під дією якого маховик зупиняється через t = 20 c.

172. Однорідний диск радіусом R = 0,2 м і масою m = 5 кг обертається навколо осі, що проходить через його центр. Залежність кутової швидкості обертання диска від часу задається рівнянням w = A + Bt, де B = 8 рад/с². Визначити величину дотичної сили, прикладеної до краю диска. Тертям знехтувати.

173. Махове колесо, яке має момент інерції 245 кг·м², обертається, роблячи 20 об./с. Через хвилину після того як на колесо перестав діяти обертальний момент, воно зупинилось. Визначити: 1) момент сил тертя; 2) кількість обертів, що зробило колесо до повної зупинки після припинення дії сил.

174. Два вантажі різної маси з'єднані ниткою і перекинуті через блок, момент інерції якого I і радіус r. За умови, що нитка не ковзає по блоку, визначити прискорення вантажів і зусилля, що діє на вісь блока, якщо маса блока дорівнює М.

175. Однорідний циліндр масою М і радіусом R обертається без тертя навколо горизонтальної осі під дією вантажу P, прикріпленого до легкої нитки, намотаної на циліндр. Визначити кут j повороту циліндра залежно від часу, якщо при t = 0 j = 0.

176. Вважати, що вантаж P (див. задачу 175) складається з двох однакових частин, зв'язаних ниткою. Визначити натяг цієї нитки Т.

177. На барабан радіусом R = 20 см, момент інерції якого I = 0,1 кг·м², намотано шнурок, до якого прив'язано вантаж масою m₁ = 0,5 кг. До початку обертання барабана висота вантажу над підлогою h₁ = 1 м. Визначити: 1) через скільки часу вантаж опуститься до підлоги; 2) кінетичну енергію вантажу в момент удару об підлогу; 3) натяг нитки. Тертям знехтувати.

178. По похилій площині, яка утворює кут a з горизонтом, скочується без ковзання суцільний однорідний диск. Визначити лінійне прискорення а центру диска.

179. По похилій площині, яка утворює з горизонтом кут a = 30⁰, скочується без ковзання суцільний однорідний циліндр, маса якого становить 300 г. Визначити величину сили тертя циліндра об площину.

180. Визначити кінетичну енергію обруча масою М, який котиться без ковзання зі швидкістю u. Товщину обруча вважати дуже малою порівняно з його радіусом.

181. Обруч і диск однакової маси котяться без ковзання з однаковою лінійною швидкістю u. Кінетична енергія обруча Е₁ = 39,2 Дж. Визначити кінетичну енергію Е₂ диска.

182. Мідна куля радіусом R = 10 см обертається з частотою 2 об./с навколо осі, що проходить через її центр. Яку роботу треба виконати, щоб збільшити кутову швидкість обертання кулі у два рази?

183. Колесо, обертаючись рівносповільнено у процесі гальмування, зменшило за 1 хв частоту обертання від 300 до 180 об/хв. Момент інерції колеса становить 2 кг·м². Визначити: 1) кутове прискорення колеса; 2) гальмівний момент; 3) роботу сил гальмування; 4) кількість обертів, зроблених колесом за цю хвилину.

184. Маховик обертається з частотою 900 об./хв. Після вимкнення маховик, обертаючись рівносповільнено, зробив до зупинки 75 об. Робота сил гальмування дорівнює 44,4 Дж. Визначити: 1) момент інерції маховика, 2) момент сил гальмування.

185. Махове колесо починає обертатись з постійним кутовим прискоренням e = 0,5 рад/с² і через t₁ = 15 с після початку руху набуває момент імпульсу L = 73,5 кг·м²/с. Визначити кінетичну енергію колеса через t₂ = 20 с після початку обертання.

186. До краю диска масою m = 5 кг прикладена постійна дотична сила F = 19,6 Н. Яку кінетичну енергію буде мати диск через Dt = 5 с після початку дії сили?

187. До візка, що стоїть на горизонтальній площині, прив'язана нитка, перекинута через блок, що закріплений на краю стола. До кінця нитки прив'язано вантаж масою m₃ = 500 г. Визначити прискорення візка а, коли відомо, що маса платформи візка m₁ = 1,4 кг, маса кожного колеса m₂ = 400 г, і колеса вважати суцільними дисками. Колеса котяться по поверхні стола без ковзання, а тертя кочення відсутнє.

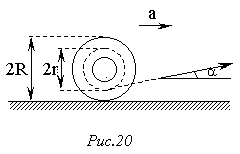
188. На горизонтальній площині знаходиться котушка з нитками. З яким прискоренням а буде рухатись вісь котушки, коли тягнути за нитку з силою F (рис.20) ? Яким чином треба тягнути за нитку, щоб котушка рухалась до натягненої нитки? Котушка рухається по поверхні стола без ковзання. Визначити силу тертя між котушкою і столом.

189. Однорідний тонкий важкий стрижень довжиною l висить на горизонтальній осі, яка проходить через один з його кінців. Яку початкову кутову швидкість w потрібно надати стрижню, щоб він повернувся на 90⁰?

190. Визначити момент імпульсу Землі L відносно її полярної осі. Вважати Землю правильною кулею радіусом R = 6400 км, яка має густину r = 5500 кг/м³.

191. Який момент сил потрібно прикласти до Землі, щоб її обертання зупинилось через 10⁸ років (рік – 366,25 доби) ?

192. На краю диска, що вільно обертається і має досить великий радіус R і момент інерції I, стоїть людина масою m. Диск робить n об./хв. Як зміниться швидкість обертання диска, якщо людина перейде від краю диска до центру? Як зміниться при цьому енергія системи? Розмірами людини у порівнянні з радіусом диска можна знехтувати.

193. Визначити, з якою мінімальною швидкістю u потрібно випустити на екваторі Землі снаряд масою m = 1000 т, щоби змінити тривалість земної доби на DТ = 1 хв?

194. Однорідний стрижень здійснює малі коливання у вертикальній площині навколо горизонтальної осі, яка проходить через його верхній кінець. Довжина стрижня l = 0,5 м. Визначити період коливань стрижня.

195. Обруч діаметром 56,5 см висить на цвяху, забитому у стіну і здійснює малі коливання у площині, паралельній стіні. Визначити період цих коливань.

§ 7. Пружні властивості тіл.