Основні теоретичні відомості. Імпульсом тіла називають добуток його швидкості на масу:

Імпульсом тіла називають добуток його швидкості на масу:

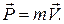
Похідна від імпульсу тіла за часом дорівнює за величиною силі, яка діє на тіло і збігається з нею за напрямком:

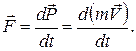
Якщо маса тіла m не змінюється з часом, то

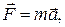
де 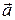– вектор прискорення тіла.

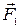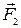Сили, з якими два тіла діють одне на одне, однакові за величиною і протилежні за напрямком. Якщо позначити ці сили і , то

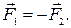
Сила тертя ковзання:

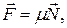
де m – коефіцієнт тертя,

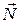– сила нормального тиску.

83. У ліфті встановлено пружинну вагу, до якої підвішене тіло масою 1 кг. Що буде показувати вага, якщо ліфт: 1) рухається вверх з прискоренням 4,9 м/с2, напрямленим вниз; 2) рухається вниз з прискоренням 4,9 м/с², напрямленим вверх; 3) рухається вниз з прискоренням 1 м/с², напрямленим вниз.

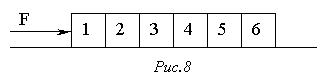
84. На гладкому горизонтальному столі розміщено шість однакових кубиків з масою m = 1 кг кожен. Постійна сила F = 9,8 H діє на перший кубик у напрямку, показаному стрілкою (рис.8). Визначити результуючу силу ¦, що діє на кожен кубик. З якою силою ¦₁ четвертий кубик діє на п'ятий?

85. На гладкій горизонтальній колії стоять п'ять вагонів масою m кожен. Постійна сила F штовхає крайній вагон. З якою силою F₁ крайній вагон діє на чотири інших вагони.

86. Автомобіль масою 1020 кг зупиняється у процесі гальмування за 5 с, проїхавши при цьому рівносповільнено відстань 25 м. Визначити початкову швидкість автомобіля і силу гальмування.

87. Яку силу потрібно прикласти до вагона, який стоїть на рейках, щоб вагон почав рухатись рівноприскорено і за час t = 30 c пройшов шлях S = 11 м? Маса вагона m = 16 т. Під час руху вагона на нього діє сила тертя, що становить 0,05 від сили тяжіння вагона.

88. Під дією постійної сили F = 9,8 Н тіло рухається прямолінійно так, що залежність пройденого тілом шляху від часу t задається рівнянням S = A – Bt + Ct². Визначити масу тіла, якщо стала С = 1 м/с².

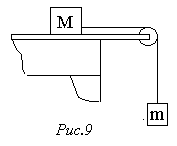
89. На гладкій горизонтальній поверхні лежить тіло масою М (рис.9). Інше тіло масою m підвішене на нитці, перекинутій через блок і прив'язаній до тіла масою М. Визначити прискорення тіл і натяг нитки. Тертям тіла масою М об площину і тертям у блоці, а також масами блоку і нитки знехтувати.

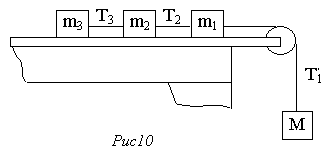
90. На гладкій горизонтальній площині розміщено три маси m₁, m₂ і m₃, зв'язані нитками між собою і з масою М, прив'язаною до нитки, перекинутої через блок (рис.10). 1) Визначити прискорення системи; 2) визначити натяг усіх ниток при тих же припущеннях, що і в задачі 89.

91. По похилій площині з кутом нахилу a ковзає тіло. Сила тертя між тілом і площиною пропорційна до сили нормального тиску тіла на площину і не залежить від швидкості тіла. Коефіцієнт тертя між тілом і площиною дорівнює к. Визначити прискорення а, з яким ковзає тіло.

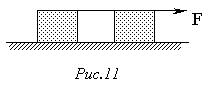
92. Два однакових тіла зв'язані ниткою і розміщені на ідеально гладкому горизонтальному столі, так що нитка утворює пряму лінію (рис.11). Нитка може витримувати натяг зі силою не більшою ніж 19,6 Н. Яку горизонтальну силу F треба прикласти до одного з тіл, щоб нитка обірвалась?

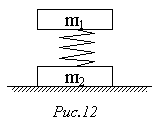
93. Дві пластинки масою m₁ і m₂ з'єднані пружиною (рис.12). З якою силою потрібно натиснути на верхню пластинку, щоб після припинення дії цієї сили верхня пластинка підскочила і підняла нижню? Масою пружини знехтувати.

94. Кінь рівномірно тягне санки. Розглянути взаємодію трьох тіл: коня, санок і поверхні землі. Нарисувати вектори сил, що діють на кожне з цих тіл окремо, і встановити співвідношення між ними.

95. Як зміниться співвідношення між силами в прикладі, розглянутому у попередній задачі, якщо кінь і санки рухаються з прискоренням а? Визначити величину всіх сил, якщо а = 0,2 м/с². Маса санок з вантажем М = 0,5 т, маса коня m = 0,35 т і коефіцієнт тертя санок об сніг 0,2.

96. На столі знаходиться дошка масою М = 1 кг, а на дошці вантаж масою m = 2 кг. Яку силу F потрібно прикласти до дошки, щоб вона вислизнула з-під вантажу? Коефіцієнт тертя між вантажем і дошкою 0,25, а між дошкою і столом 0,5.

97. Повітряна куля масою М опускається зі сталою швидкістю. Яку кількість баласту DМ треба викинути, щоб куля почала підійматись з тією ж швидкістю? Підіймальну силу P кулі вважати сталою.

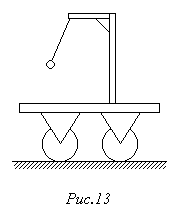
98. Маятник масою m підвішений до підставки, закріпленої на візку (рис.13). Визначити напрям нитки маятника, тобто кут a нитки маятника з вертикаллю, і її натяг T у таких випадках: 1) візок рівномірно рухається по горизонтальній площині; 2) візок рухається горизонтально з прискоренням а; 3) візок вільно скочується з похилої площини, яка утворює кут j з горизонтом; 4) візок з деяким прискоренням b, напрямленим уздовж похилої площини, вкочується на неї; 5) візок з тим же прискоренням b скочується з похилої площини.

99. На автомобіль з масою 1 т під час руху діє сила тертя, що дорівнює 0,1 від його сили тяжіння. Визначити силу тяги, яку створює двигун автомобіля, якщо автомобіль рухається зі сталою швидкістю: 1) догори з нахилом 1 м на кожні 25 м шляху; 2) вниз з тим же нахилом.

100. Тіло ковзає по похилій площині, яка утворює з горизонтом кут a = 45⁰. Пройшовши відстань S = 36,4 см тіло набуває швидкості u = 2 м/с². Визначити коефіцієнт тертя тіла об площину.

101. Тіло ковзає по похилій площині, яка утворює з горизонтом кут a = 45⁰. Залежність пройденого шляху S від часу t задається рівнянням S = Ct², де С = 1,73 м/с². Визначити коефіцієнт тертя тіла об площину.

102. Камінь кинули вертикально вгору. У яких точках траєкторії камінь буде мати максимальне прискорення? Розглянути два випадки: 1) опір повітря відсутній; 2) опір повітря збільшується внаслідок збільшення швидкості каменя.

103. Дві гирі з масами m₁ = 2 кг і m₂ = 1 кг з'єднані ниткою і перекинуті через невагомий блок. Визначити: 1) прискорення, з яким рухаються гирі; 2) натяг нитки; 3) силу, що діє на вісь блока. Тертям у блоці знехтувати.

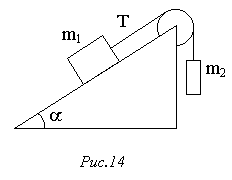
104. На верхньому краю ідеально гладкої похилої площини закріплено блок, через який перекинуто нитку (рис.14). На одному її кінці прив'язано вантаж з масою m₁, який знаходиться на похилій площині. На другому кінці висить вантаж з масою m₂. З яким прискоренням а рухаються вантажі і який натяг T нитки? Похила площина утворює з горизонтом кут a.

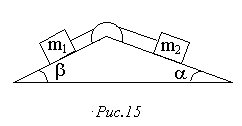
105. Невагомий блок закріплено на вершині двох похилих площин, які утворюють з горизонтом кут a = 30⁰ і b = 45⁰ (рис.15). Гирі однакової маси m₁ = m₂ = 1 кг з'єднані ниткою і перекинуті через блок. Визначити: 1) прискорення, з яким рухаються гирі; 2) натяг нитки. Тертям гир об похилі площини, а також тертям у блоці знехтувати.

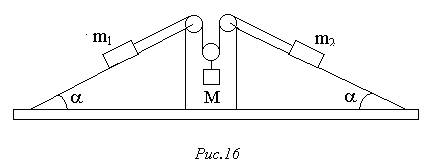
106. Визначити прискорення маси М у системі, зображеній на рис.16. Масою блоків і силами тертя знехтувати. Клини вважати закріпленими жорстко.

107. Через блок, описаний у задачі 103, перекинуто нитку і деякі маси m₁ та m₂ рухаються. За проміжок часу t після початку руху маса m₁ опустилась на n‑ту частину тієї відстані, яку вона пройшла б за той же час при вільному падінні. Яке відношення мас m₁ і m₂?

108. Кожен з обох вантажів на блоці, описаному у задачі 103, має масу m = 250 г. На один з вантажів покладено додаткову масу Dm = 5 г. Визначити час t від початку руху, протягом якого кожен вантаж пройде шлях S = 1 м, а також швидкість u, яку будуть мати вантажі після проходження цієї відстані.

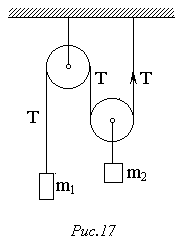
109. Визначити прискорення а₁ і а₂ мас m₁ і m₂ та натяг нитки Т у системі, зображеній на рис.17. Масою блоків і ниток знехтувати.

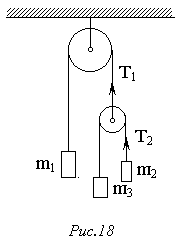
110. Визначити прискорення маси m₁ і натяги ниток Т₁ і Т₂ у системі, зображеній на рис.18. Масою блоків і ниток знехтувати, сил тертя не враховувати.

111. Дві кульки падають у повітрі. Кульки суцільні, зроблені з одного матеріалу, але діаметр однієї з кульок удвічі більший від іншої. У якому співвідношенні будуть перебувати швидкості кульок у випадку встановленого рівномірного руху? Вважати, що сила опору повітря пропорційна до площі поперечного перерізу рухомого тіла і до квадрата його швидкості?

112. Стальна кулька радіусом 0,05 мм падає в широку посудину, наповнену гліцерином. Визначити швидкість u встановленого рівномірного руху кульки. Коефіцієнт внутрішнього тертя у гліцерині дорівнює h = 1,0 Па·с, густина гліцерину r₁ = 1260 кг/м³, густина сталі r₂ = 7800 кг/м³.

Вказівка. Для розв'язку задачі скористатись гідродинамічною формулою Стокса, яка визначає силу опору, що зазнає кулька під час руху у в'язкій рідині: ¦ = 6pruh.

113. Як змінюватиметься швидкість тіла, яке рухається вертикально вверх з початковою швидкістю u₀, якщо приймати, що сила опору повітря пропорційна до швидкості тіла?

114. З однієї нерухомої хмари через t с одна за одною починають падати дві дощові краплі. Як буде змінюватись з часом відстань між ними? Розв'язати задачу для двох випадків: 1) приймаючи, що опір повітря відсутній; 2) приймаючи, що опір повітря пропорційний до швидкості крапель.

115. Моторний човен розвинув швидкість u₀. 1) як буде зменшуватись з часом швидкість руху човна у стоячій воді після вимкнення двигуна, якщо опір води щодо руху човна можна вважати пропорційним до квадрата швидкості? 2) скільки часу буде рухатись човен? 3) Який шлях він пройде до повної зупинки?

116. Розглянути питання, поставлені у попередній задачі у припущенні, що опір води рухові човна пропорційний до першого степеня його швидкості.

117. Який буде період малих коливань математичного маятника довжини l, якщо маятник коливається у вагоні, що їде в горизонтальному напрямку з прискоренням а?

118. Який буде період малих коливань маятника у ліфті, що опускається з постійним прискоренням а? Яким буде період коливань маятника при а = g? Як поведе себе маятник при а > g?

§ 4. Робота й енергія, потужність.