Основні теоретичні відомості. де с – швидкість світла в вакуумі.

Перетворення Лоренца

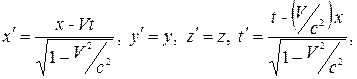
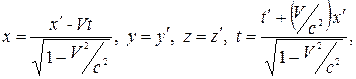
де с – швидкість світла в вакуумі.

Позначення зі штрихом відносяться до просторово-часових координат системи відліку, що рухається відносно нерухомої системи координат з швидкістю V у додатному напрямі осі x, при чому осі x' і х збігаються, а осі y' і y, z' і z паралельні.

Сповільнення ходу рухомого годинника:

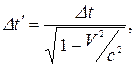
де Dt' – інтервал часу між подіями в рухомій системі відліку;

Dt – інтервал часу між цими ж подіями в нерухомій системі.

Скорочення довжини рухомого тіла:

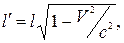
де l' – довжина рухомого тіла;

l – власна довжина.

Релятивістський закон додавання швидкостей:

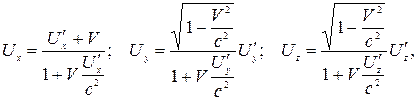
де U_x, U_y, U_z – проекції швидкості в нерухомій системі координат;

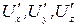– проекції швидкості в рухомій системі.

Релятивістська маса й імпульс:

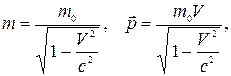
де m₀ – маса спокою.

Повна енергія тіла:

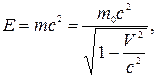
де E₀ = m₀c² – енергія спокою.

Кінетична енергія тіла в релятивістському випадку:

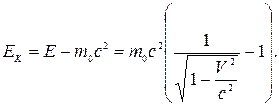
71. Вздовж осі X інерціальної системи відліку К рухається ракета зі швидкістю u = 0,9с (с – швидкість світла), яка проходить початок координат О в момент часу t = 0. У момент t₁ = 9 c за ракетою посилається світловий сигнал з точки О, а з ракети – світловий сигнал у точку О. Вважаючи, що ракета рухається у вакуумі, знайти: 1) момент часу t₂, коли світловий сигнал, посланий з точки О, досягне ракети; 2) момент часу t₃, коли сигнал, посланий з ракети, прийде в точку О; 3) на якій відстані x₂ від точки О перебуватиме ракета, коли до неї прийде сигнал з точки О; 4) коли вернеться в точку О посланий з неї сигнал, якщо він відіб’ється від дзеркала, встановленого на ракеті (момент часу t₄­)?

72. Знайти зв'язок між проміжком власного часу між двома подіями і проміжком часу між цими ж двома подіями в іншій інерціальній системі відліку, у якій ці дві події відбуваються у різних точках, з допомогою такого експерименту.

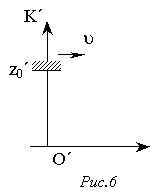
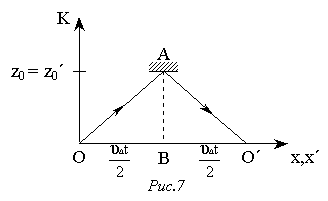
У системі К^¢ на осі z^¢ на відстані z^¢₀ від початку відліку О^¢ закріплене дзеркало (рис.6). З джерела, розташованого в О^¢, вздовж z^¢ направляють світловий сигнал, посилання і зворотний прихід якого фіксується годинником, який перебуває у стані спокою в О^¢. Цей годинник відраховує проміжок власного часу Dt₀. Ці ж дві події розглянути в системі К (рис.7) і визначити проміжок часу між цими двома подіями в заданій системі. Вважаючи, що в момент посилання сигналу початки відліку О та О^¢ збігаються, а годинники у цей момент в обох системах у точці, де збігаються початки О і О^¢, відраховують моменти часу t = 0 і t^¢= 0, знайти покази годинників у системах К і К^¢ для моменту повернення сигналу.

73. Космічний корабель зі сталою швидкістю u = (24/25)с рухається в напрямку до центра Землі. Яку відстань у системі відліку, зв'язаною із Землею, пройде корабель за проміжок часу Dt¢ = 7c, відрахований за корабельним часом? Обертання Землі та її орбітальний рух не враховувати.

74. Космонавт перебуває у неосвітленому космічному кораблі, який рухається відносно Землі зі швидкістю, дуже близькою до швидкості світла с. На невеликій відстані від космонавта розташоване дзеркало так, що лінія, яка з'єднує космонавта і дзеркало, паралельна до швидкості корабля. Чи побачить космонавт своє зображення в дзеркалі після ввімкнення джерела світла, розташованого поряд з космонавтом? (Загадка Ейнштейна).

75. З початку відліку системи К уздовж осі X через інтервал часу Т (за годинником К) посилаються короткочасні світлові імпульси. Знайти інтервал часу, через який ці імпульси будуть приходити до спостерігача в системі К^¢, враховуючи також відносність проміжків часу між подіями (див. задачу 72). Розглянути випадки віддалення і зближення спостерігача і джерела. Перейшовши від періодів до частот, отримати релятивістські формули для повздовжнього ефекту Доплера.

76. Використовуючи перетворення Лоренца, довести, що: 1) дві події, які одночасно відбуваються в одній системі відліку К, в усіх інших системах відліку відбуваються в різні моменти часу (за умови, що вони не відбуваються в одній і тій же точці системи К); 2) дві події, які відбуваються в одній і тій же точці системи К, у всіх інших системах відліку відбуваються в точках, що мають різні координати (за умови, що в системі К вони не відбулись одночасно).

77. Нерухомий у системі К спостерігач може виміряти довжину рухомого стержня таким чином. Нехай стержень орієнтований уздовж спільної осі x, x^¢ і перебуває в стані спокою в К^¢. Спостерігачеві з К відома швидкість системи К^¢– u. У руках спостерігача годинник, за яким він визначає моменти проходження повз нього початку і кінця стержня t₁ та t₂, і нехай Dt = t₂-t₁. Тоді він вважає довжиною стержня u(t₂-t₁). Довести, що і у випадку такого визначення довжини справедлива формула 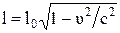, де l₀ – власна довжина стержня.

78. Стержень, власна довжина якого дорівнює l₀, перебуває у спокої в системі відліку К¢. Він розташований так, що створює з віссю x¢ кут j¢. Який кут створює цей стержень з віссю х другої системи відліку К? Яка довжина цього стержня в системі К?

79. Стержень, власна довжина якого дорівнює l₀, розташований паралельно осі x і рухається у додатньому напрямку осі y. Його швидкість у системі К дорівнює w. У системі К¢ цей стержень стає дещо нахиленим відносно додатнього напрямку осі х¢. Пояснити цей результат, не використовуючи перетворення Лоренца. Нехай центр стержня проходить через точку x = 0, y = 0, x¢ = 0, y¢ = 0 у момент часу t = t¢ = 0. Визначити кут j¢, який утворює стержень з віссю x¢ у системі К¢.

80. Нехай у системі К рух частинки задано виразами: x = x(t), y = y(t), z = z(t). Визначаючи швидкість звичайними формулами, наприклад, u_x = dx/dt та іншими , та застосовуючи перетворення Лоренца, знайти формули перетворення компонент швидкостей у випадку переходу від системи відліку К до системи K¢, де відповідно u_x¢ = dx¢/dt¢ і т.д.

81. Порівняти величину релятивістського і класичного імпульсів електрона при швидкості u = (24/25)c = 0,96 c.

82. Виразити релятивістський імпульс частинки, маса якої дорівнює m, через її релятивістську кінетичну енергію.

§ 3. Динаміка прямолінійного руху.