Основні теоретичні відомості.

Кінематика

Миттєва швидкість:

.

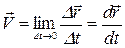Модуль швидкості:

,

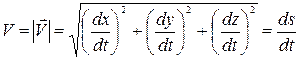де ds – шлях, пройдений точкою за час dt.

Миттєве прискорення:

.

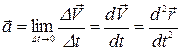Модуль прискорення:

.

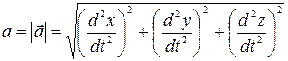У випадку прямолінійного рівномірного руху:

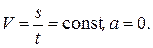
У випадку прямолінійного рівнозмінного руху:

.

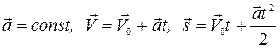У цих рівняннях прискорення а додатне у випадку рівноприскореного руху і від'ємне у випадку рівносповільненого.

Повне прискорення у випадку криволінійного руху:

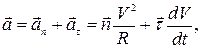
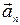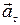де і – нормальне (доцентрове) і тангенціальне (дотичне) прискорення;

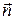і 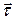– одиничні вектори в напрямку нормалі і дотичної до траєкторії відповідно;

R – радіус кривизни траєкторії.

Кутова швидкість і кутове прискорення у випадку обертового руху:

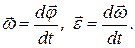
Зв'язок кутової швидкості w з лінійною швидкістю V:

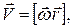
де 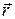– радіус-вектор матеріальної точки відносно довільної точки на осі обертання.

У випадку рівномірного обертового руху кутова швидкість:

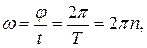
де Т – період обертання;

n – частота обертання, тобто кількість обертів за одиницю часу.

Тангенціальне і нормальне прискорення у випадку обертового руху:

a_t = eR, a_n = w²R.

Закон додавання швидкостей Галілея:

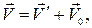
де 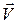– швидкість матеріальної точки в умовно нерухомій системі координат (абсолютна швидкість);

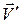– її швидкість у рухомій системі координат (відносна швидкість);

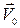– швидкість рухомої системи координат відносно нерухомої.

1. Першу половину часу свого руху автомобіль рухався зі швидкістю 80 км/год, а другу – 40 км/год. Яка середня швидкість руху автомобіля?

2. Першу половину свого шляху автомобіль рухався зі швидкістю 80 км/год, а другу – 40 км/год. Яка середня швидкість руху автомобіля?

3. Визначити швидкість відносно берега річки: 1) човна, який пливе за течією; 2) човна, який пливе проти течії; 3) човна, який пливе під кутом a = 90⁰ до течії. Швидкість течії річки u₁ = 1 м/с, швидкість човна відносно води u₂ = 2 м/с.

4. Камінь кинули вверх на висоту 10 м. 1) через скільки часу він впаде на землю? 2) на яку висоту підійметься камінь, якщо початкову швидкість збільшити вдвічі? Опором повітря знехтувати.

5. Побудувати графік залежності висоти h і швидкості u від часу t для тіла, кинутого вертикально вверх з початковою швидкістю 9,8 м/с. Графік побудувати для інтервалу часу від 0 до 2 с, через кожні 0,2 с. Опір повітря не враховувати.

6. Тіло падає вертикально з висоти h = 19,6 м з нульовою початковою швидкістю. Який шлях пройде тіло: 1) за першу 0,1 с свого руху, 2) за останню 0,1 с свого руху ? Опір повітря не враховувати.

7. Швидкість тепловоза, який у процесі гальмування рухається рівносповільнено, зменшується протягом 1 хв від 40 до 28 км/год. Визначити: 1) від'ємне прискорення тепловоза; 2) відстань, яку пройде тепловоз за час гальмування.

8. Вагон рухається рівносповільнено з від'ємним прискоренням ‑ 0,5 м/с². Початкова швидкість вагона 54 км/год. За який час і на якій відстані від початкової точки вагон зупиниться ?

9. Залежність пройденого тілом шляху S від часу t задається рівнянням S = At – Bt² + Ct³, де A = 2 м/с, B = 3 м/с², С = 4 м/с³. Визначити: 1) залежність швидкості u і прискорення а від часу t; 2) відстань, яку пройшло тіло, швидкість і прискорення тіла через 2 с після початку руху. Побудувати графік шляху, швидкості і прискорення для 0 £ t £ 3 c через 0,5 с.

10. Залежність пройденого тілом шляху S від часу t задається рівнянням S = A + Bt + Ct², де A = 3 м, B = 2 м/с, С = 1 м/с². Визначити середню швидкість і середнє прискорення тіла за першу, другу і третю секунди його руху.

11. Колесо, обертаючись рівноприскорено, досягло кутової швидкості w = 20 рад/с через N = 10 обертів після початку обертання. Визначити кутове прискорення колеса.

12. Махове колесо через t = 1 хв після початку руху набуває швидкості, що відповідає частоті n = 720 об./хв. Визначити кутове прискорення колеса та кількість обертів колеса за цю хвилину. Рух вважати рівноприскореним.

13. Колесо, обертаючись рівносповільнено, у процесі гальмування зменшило свою частоту за 1 хв від 300 до 180 об./хв. Визначити кутове прискорення колеса і кількість обертів, зроблених ним за цей час.

14. Якір електродвигуна обертається зі швидкістю, що відповідає частоті 900 об./хв. Після вимкнення двигуна якір, обертаючись рівносповільнено, зробив до зупинки 75 об. Скільки часу минуло з моменту вимкнення двигуна до повної зупинки якоря ?

15. Вал обертається зі сталою швидкістю, що відповідає частоті 180 об./хв. З деякого моменту вал гальмується й обертається рівносповільнено з кутовим прискоренням, що дорівнює 3 рад./с². 1) за який час вал зупиниться? 2) скільки обертів він зробить до зупинки?

16. Колесо радіусом R = 10 см обертається зі сталим кутовим прискоренням e = 3,14 рад./с². Визначити для точок на поверхні колеса до кінця першої секунди після початку руху: 1) кутову швидкість, 2) лінійну швидкість, 3) тангенціальне прискорення, 4) нормальне прискорення, 5) повне прискорення, 6) кут, що утворюється між напрямом повного прискорення і радіусом колеса.

17. Визначити кутове прискорення колеса, якщо відомо, що через 2 с після початку рівноприскореного руху вектор повного прискорення точки, яка знаходиться на краю колеса, створює кут 60⁰ з напрямком лінійної швидкості цієї точки.

18. Колесо радіусом R = 5 см обертається так, що залежність кута повороту радіуса колеса від часу задається рівнянням j = A + Bt + Ct² + Dt³, де D = 1 рад./с³. Визначити для точок на краю колеса зміну тангенціального прискорення Da_t за кожну секунду руху.

19. Колесо обертається так, що залежність кута повороту радіуса колеса від часу задається рівнянням j = A + Bt + Ct² + Dt³, де B = 1 рад./с, C = 1 рад/с² і D = 1 рад/с³. Визначити радіус колеса, якщо відомо, що до кінця другої секунди руху нормальне прискорення точок на краю колеса дорівнює а_n = 3,46·10² м/с².

20. Колесо обертається зі сталим кутовим прискоренням e = 2 рад./с². Через t = 0,5 с після початку руху повне прискорення колеса а = 13,6 см/с². Визначити радіус колеса.

21. На платформі, що рівномірно рухається по горизонтальній площині, встановлено трубу. Як повинна бути орієнтована на платформі ця труба, щоб краплі дощу, які падають вертикально, пролітали через неї, не торкаючись внутрішніх стінок? Рух крапель вважати рівномірним.

22. Корабель пливе на захід зі швидкістю 6,5 м/с. Вітер дує з південного заходу зі швидкістю 3,5 м/с. Яку швидкість вітру u зареєструють прилади, розташовані на кораблі? Який напрям вітру відносно курсу корабля покажуть ці прилади?

23. Два літаки одночасно вилітають з одного місця у двох взаємно перпендикулярних напрямках. Один зі швидкістю u₁ = 300 км/год, другий – u₂ = 400 км/год. Як збільшується з часом відстань між літаками? Чому дорівнює ця відстань S у момент, коли перший літак пролетів шлях S₁ = 900 км?

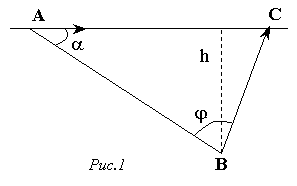
24. Людина, яка знаходиться в точці B на відстані h від прямої ділянки дороги (рис.1), бачить в точці А автобус, що їде по дорозі зі сталою швидкістю u_a. Відстань від людини до автобуса в цей момент – AB. У якому напрямку треба бігти людині, щоб опинитись на дорозі в точці C з максимальним випередженням за часом відносно до автобуса? Відношення відстаней h/AB = 1/2, а відношення швидкостей людини й автобуса u_Л/u_a = 1/ .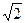

25. Між двома пунктами, розташованими на ріці на відстані L = 100 км один від одного, курсує катер. Катер проходить цю відстань за течією за час t = 4 год, а проти течії – t₂ = 10 год. Визначити швидкість течії річки u₁ і швидкість катера відносно води u₂.

26. Рибалка пливе човном вверх по ріці. Пропливаючи під мостом, він губить у воді гарпун. Через півгодини рибалка це помічає і, повертаючи назад, доганяє гарпун на 5 км нижче від мосту. Яка швидкість течії ріки, якщо рибалка, рухаючись вверх і вниз по ріці, веслував однаково?

27. Тіло, рухаючись зі сталим прискоренням, проходить послідовно два однакові відрізки шляху S по 10 м кожен. Визначити прискорення тіла а і швидкість V₀ на початку першого відрізку, якщо перший відрізок пройдений тілом за час t₁ = 1,06 с, а другий за t₂ = 2,2 с.

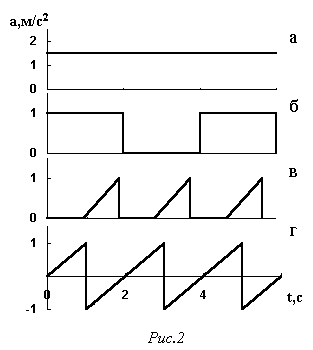
28. Побудувати графіки залежності від часу швидкості деяких тіл, якщо графіки прискорення а цих тіл мають вигляд, зображений на рис.2. Прийняти, що початкова швидкість тіл у всіх випадках дорівнює нулю.

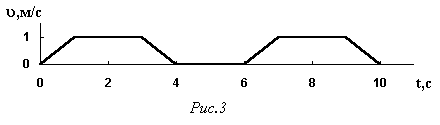
29. Накреслити графіки залежності від часу шляху та прискорення деякого тіла, якщо швидкість цього тіла як функція часу зображена на рис.3.

30. Яка допустима гранична швидкість u приземлення парашутиста, якщо людина може безпечно скакати з висоти до h = 2 м?

31. З вишки одночасно кинуто два тіла з однаковою початковою швидкістю u₀: одне вертикально вверх, друге вертикально вниз. Як з часом буде змінюватись відстань S між цими тілами? Опір повітря руху тіл не враховувати.

32. На яку максимальну відстань l можна кинути м'яч у спортивному залі висотою 8 м, якщо м'яч має початкову швидкість 20 м/с? Який кут j з підлогою залу повинен у цьому випадку становити вектор початкової швидкості м'яча? Прийняти, що висота початкової точки траєкторії м'яча над підлогою дуже мала порівняно з висотою залу. М'яч під час польоту не повинен вдарятись об стелю залу. Опором повітря у процесі руху м'яча знехтувати.

33. Літак летить на висоті h горизонтально по прямій лінії з швидкістю u. Пілот повинен скинути бомбу в ціль, розташовану перед літаком. Під яким кутом a до вертикалі він повинен бачити ціль у момент випуску бомби? Яка в цей момент відстань l від цілі до точки, над якою розташований літак? Опір повітря під час руху бомби не враховувати.

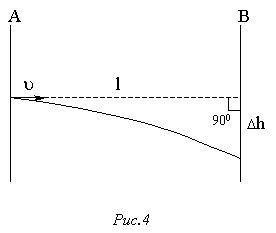
34. Швидкість кулі можна визначити за пониженням її траєкторії Dh на заданій відстані l у випадку горизонтального пострілу. Пониження траєкторії визначається за отворами, зробленими кулею у двох вертикальних послідовно встановлених на шляху кулі щитах A і B (рис.4). Визначити швидкість кулі, вважаючи Dh і l відомими та нехтуючи опором повітря.

35. Ціль, розміщену на пагорбі, видно з місця розташування гармати під кутом a до горизонту. Відстань по горизонталі від гармати до цілі дорівнює l. Постріл по цілі здійснюється при куті підвищення b. Визначити початкову швидкість u₀ снаряда, який попадає в ціль. Опір повітря не враховувати.

36. Матеріальна точка ковзає без тертя по довільній похилій площині. Довести, що після того, як точка опуститься на висоту h, швидкість її буде такою ж, як і у випадку вільного її падіння з тієї ж висоти h.

37. Човен, який перепливає річку на веслах, переміщується відносно води зі швидкістю 2 м/с у напряку, перпендикулярному до течії. Течія річки має швидкість 1 м/с. Знайти швидкість човна у стоячій воді і напрямок вектора цієї швидкості відносно берега річки.

38. Вагонетка повинна перевезти вантаж у найкоротший термін з однієї точки в іншу, які знаходяться на відстані l. Вагонетка може розганятися або сповільнювати хід лише з однаковим за величиною і сталим у часі прискоренням, а потім переходить або в рівномірний рух, або зупиняється. Якої найбільшої швидкості u повинна досягти вагонетка, щоб була виконана поставлена вище умова?

39. З точки, яка знаходиться на верхньому кінці вертикального діаметра кола, по жолобках, які розміщені вздовж різних хорд цього кола, одночасно починають зісковзувати без тертя вантажі. Довести, що всі вантажі одночасно досягнуть лінії кола.

40. Човен, що рухався зі швидкістю u₀, опускає вітрило в момент часу t₀, але продовжує рухатися. Під час цього руху виявлено гіперболічну залежність швидкості човна від часу u » 1/t. Довести, що прискорення човна а було пропорційне до квадрата швидкості.

41. Користуючись умовами попередньої задачі, знайти залежності: а) шляху S, пройденого човном, від часу t; б) швидкості човна u від шляху після опускання вітрила.

42. Визначити рівняння траєкторії, швидкість і прискорення тіла, координати якого так залежать від часу: x = ct², y = dt², (с і d – додатні постійні).

43. З пароплава, який рухається зі швидкістю u₁, випущено вертикально вгору снаряд з початковою швидкістю u₀. Знайти величину і напрямок вектора швидкості u снаряда залежно від часу і рівняння траєкторії снаряда в нерухомій системі відліку. Опором повітря знехтувати.

44. Камінь кинуто з висоти 2,1 м під кутом a = 45⁰ до горизонту. На відстані 42 м по горизонталі від місця кидання камінь падає на землю. Знайти початкову швидкість каменя, час польоту і максимальну висоту підняття над землею. Визначити радіуси кривизни траєкторії у верхній точці і в точці падіння каменя на землю.

45. Літак летить горизонтально зі швидкістю u. У напрямку руху з літака випускають снаряд зі швидкістю u₀. Знайти рівняння траєкторії снаряда відносно землі і відносно літака. Опором літака знехтувати.

46. Яку початкову швидкість u₀ повинна мати сигнальна ракета, випущена з ракетниці під кутом 45⁰ до горизонту, щоб вона спалахнула у найвищій точці своєї траєкторії, якщо час горіння запалу ракети становить 6 с? Опір повітря руху ракети не враховувати.

47. Місяць обертається навколо Землі з періодом Т = 27,3 доби відносно зірок. Середній радіус орбіти Місяця R = 3,8·10⁵ км. Визначити лінійну швидкість u руху Місяця навколо Землі та його нормальне прискорення а_n.

48. Знайти середню лінійну швидкість штучного супутника Землі, якщо період його обертання по орбіті становить 111 хв, а середня висота польоту 1200 км.

49. Визначити лінійну швидкість u точок земної поверхні на географічній широті j, спричинену добовим обертанням Землі навколо своєї осі. Радіус земної кулі R = 6400 км.

50. Знайти швидкість, з якою рухається тінь Місяця по земній поверхні під час повного сонячного затемнення, якщо воно спостерігається на екваторі. Для спрощення прийняти, що площини сонячної та місячної орбіт (відносно Землі) збігаються, а земна вісь до них перпендикулярна. Швидкість світла вважати безмежно великою у порівнянні з усіма іншими даними у задачі швидкостями. Радіус місячної орбіти R_м = 3,8·10⁵ км.

51. У відкритому морі на екваторі височить висока вертикальна скеля. Як буде рухатись по скелі тінь, що падає від сферичної поверхні Землі під час заходу Сонця? Визначити прискорення такого руху. Радіус Землі R = 6400 км. За який час тінь переміститься від основи до вершини скелі, якщо її висота h = 1 км?

52. Якір електродвигуна, що обертається з частотою n обертів за секунду, рухаючись після вимкнення струму рівносповільнено, зупинився, зробивши n обертів. Визначити кутове прискорення якоря після вимкнення струму.

53. Автомобіль рухається зі швидкістю 60 км/год. Скільки обертів за секунду роблять його колеса, якщо вони котяться по шосе без ковзання, а зовнішній діаметр коліс дорівнює 60 см? Знайти величину нормального прискорення зовнішнього шару гуми на поверхні коліс.

54. Розмотуючи шнурок і обертаючи без ковзання вал, відро опускається в колодязь з прискоренням 1 м/с². З яким кутовим прискоренням обертається вал? Як залежить від часу кут повороту вала? Радіус вала дорівнює 25 см.

55. Автомобіль, що рухається зі швидкістю 40 км/год, проходить заокруглення шосе з радіусом кривизни 200 м. На повороті водій гальмує машину, надаючи їй прискорення 0,3 м/с². Визначити нормальне і повне прискорення автомобіля на повороті. Як напрямлений вектор повного прискорення відносно до радіуса кривизни R заокруглення шосе.

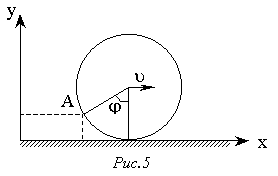
56. Колесо радіусом R рівномірно котиться без ковзання по горизонтальному шляху зі швидкістю u. Визначити координати x та y довільної точки А на ободі колеса, виразивши їх як функції часу t або кута повороту колеса j, приймаючи, що при t = 0 j = 0, x = 0, y = 0 (рис.5). За знайденими виразами для x та y побудувати графік траєкторії точки на ободі колеса.

57. Автомобіль з колесами радіусом R рухається зі швидкістю u по горизонтальній дорозі, причому u² > Rg, де g – прискорення вільного падіння. На яку максимальну висоту h може бути закинене вверх болото, що відривається від коліс автомобіля? Вказати положення тієї точки на поверхні колеса, з якої при даній швидкості руху автомобіля болото буде закидатись найвище. Опором повітря під час руху закинутого вверх болота знехтувати.

58. В якій точці траєкторії тіла, що кинуте під кутом до горизонту, його нормальне до траєкторії прискорення буде максимальним? Опір повітря не враховувати.

59. Матеріальна точка починає рух по колу, радіус якого дорівнює 0,1 м. Точка рухається зі сталим тангенціальним прискоренням а_t = 4·10³ м/с². Через скільки часу вектор прискорення а утворить з вектором швидкості u кут a = 60⁰? Який шлях пройде точка за цей час. На який кут повернеться радіус-вектор, якщо у початковий момент часу він з центра кола спрямований вертикально догори? Рух відбувається за годинниковою стрілкою.

60. Деяке тверде тіло одночасно обертається з кутовими швидкостями w₁, w₂ = 2w_1, w₃ = 3w₁ навколо трьох взаємноперпендикулярних миттєвих осей, що проходять через одну точку. Визначити, як повинна бути спрямована відносно до названих осей вісь, обертання навколо якої могло б замінити зразу всі три вказані незалежні обертання?

61. З вежі висотою H = 25 м горизонтально кинули камінь зі швидкістю u₀ = 15 м/с. Визначити: 1) скільки часу камінь перебуватиме в русі, 2) на якій відстані S_x від основи вежі він впаде на землю, 3) з якою швидкістю u він впаде на землю; 4) який кут j утворює траєкторія каменя з горизонтом у точці його падіння на землю. Опір повітря не враховувати.

62. М'яч, кинутий горизонтально, вдаряється в стінку, розташовану на відстані 5 м від місця кидання. Висота місця удару м'яча до стінки на 1 м менша від висоти, з якої кинуто м'яч. 1) з якою швидкістю u₀ кинуто м'яч? 2) під яким кутом j м'яч підлітає до поверхні стінки? Опір повітря не враховувати.

63. Камінь кинуто в горизонтальному напрямку. Через 0,5 с після початку руху числове значення швидкості каменя стало у 1,5 раза більше від його початкової швидкості. Визначити початкову швидкість каменя. Опір повітря не враховувати.

64. Тіло кинуте зі швидкістю u₀ = 14,7 м/с під кутом a = 30⁰ до горизонту. Визначити нормальне і тангенціальне прискорення тіла через t = 1,25 с після початку руху. Опір повітря не враховувати.

65. Тіло кинуте зі швидкістю u₀ під кутом a до горизонту. Визначити величини u₀ і a, якщо відомо, що найбільша висота підйому тіла h = 3 м. Опір повітря не враховувати.

66. З вежі висотою H = 25 м кинули камінь зі швидкістю u₀ = 15 м/с під кутом a = 30⁰ до горизонту. Визначити: 1) скільки часу камінь перебуватиме в русі; 2) на якій відстані від основи вежі він упаде на землю; 3) з якою швидкістю він упаде на землю; 4) який кут утворить траєкторія каменя з горизонтом у точці його падіння на землю. Опір повітря не враховувати.

67. З гармати здійснили постріл під кутом j до горизонту. Величина початкової швидкості снаряда u₀. Дослідити аналітично рух снаряда, нехтуючи опором повітря і кривизною поверхні Землі. Визначити: 1) вертикальну і горизонтальну компоненти вектора швидкості u і абсолютну величину швидкості як функцію часу; 2) час t польоту снаряда від гармати до падіння на землю; 3) залежність від часу кута a між вектором швидкості снаряда і горизонтом; 4) декартові координати x і y як функції часу; 5) рівняння траєкторії снаряда y = ¦(x).

68. З трьох труб, розташованих на землі, з однаковою швидкістю витікають потоки води під кутом 60, 45 і 30⁰ до горизонту. Визначити відношення найбільших висот h підйому потоків води, що витікають з кожної труби, і відношення дальностей падіння l води на землю. Опір повітря не враховувати.

69. Які будуть графіки залежності від часу абсолютних величин швидкості і прискорення у випадку рівномірного руху точки по колу?

70. Радіолокаційні дослідження виявили, що Венера обертається навколо своєї осі в напрямку, оберненому до її орбітального руху. Період осьового обертання Венери (відносно зірок) T₁ = 243 земних доби. Венера обертається навколо Сонця з періодом T₂ = 225 земних діб. Визначити тривалість сонячної доби на Венері, тобто час t між двома послідовними проходженнями Сонця через один і той же меридіан на цій планеті.

§ 2. Спеціальна теорія відносності.