Связь между суммой по состояниям и термодинамическими функциями

Напомним, что сумма по состояниям представляет собой сумму всех возможных значений фактора Больцмана для данной системы

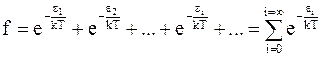. (11 - 29)

Дифференцирование уравнения (11 - 29) по температуре при постоянном объеме дает

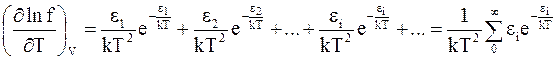
Разделив обе части равенства на f и умножив на kT², получим

..

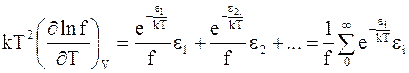Умножение на N приводит к следующему равенству:

,

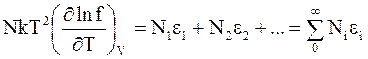правая часть которого представляет внутреннюю энергию системы.

Следовательно,

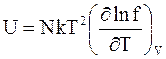. (11 - 30)

Из уравнений (11 - 16а) и (11 - 17) найдем

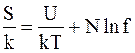. (11 - 31)

Откуда

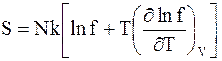. (11 - 32)

Таким образом, методы статистической термодинамики дают возможность рассчитывать термодинамические функции по суммам по состояниям. Вычисление энтальпии, энергии Гельмгольца и энергии Гиббса не составит труда, если известны внутренняя энергия и энтропия системы.

Так как молекулы находятся одновременно в поступательном, вращательном, колебательном и др. движениях, то сумма по состояниям определяется этими составляющими. В простейших молекулах эти виды движения можно принять независимыми и возможен расчет для отдельных форм движения с использованием квантово-механических представлений.

Экспериментальной базой для вычисления сумм по состояниям служат спектры молекул.

Глава 12. Основные понятия термодинамики неравновесных процессов