Приложения. Полный дифференциал функции нескольких переменных

Полный дифференциал функции нескольких переменных

Пусть F является функцией переменных Х₁,Х₂,... ...Хi, ...

Частные производные этой функции равны

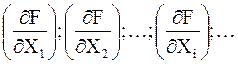
Частные дифференциалы функции F представляют собой произведение частной производной на приращение независимой переменной

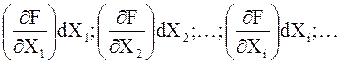
Полный дифференциал является суммой частных дифференциалов

.

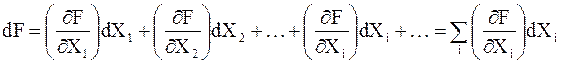Бесконечно малое приращение какой-либо величины, определяемое бесконечно малыми приращениями других величин, не всегда является полным дифференциалом. Например, в приведенном ниже выражении dz не является полным дифференциалом

.

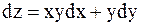Для равенства с двухчленной правой частью, содержащей бесконечно малые приращения переменных (типа приведенного выше),

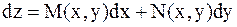, (а)

сравнительно легко установить, является ли приращение dz полным дифференциалом. Используя свойство частных производных

,

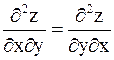в случае, если выполняются условия

,

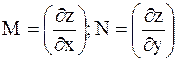получим

.

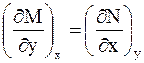Известна теорема Коши, согласно которой любое равенство типа (а) можно перевести в форму полного дифференциала умножением обеих частей равенства на функцию l=l(x,y) или делением на функцию m=m(x,y). Функция l называется интегрирующим множителем, а функция m - интегрирующим делителем. Естественно, что m=1/l.

Однородные функции первой степени. Формула Эйлера

Однородными функциями называются функции

,

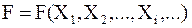для которых выполняется условие

,

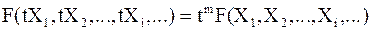где m - степень функции.

При m=1 функция называется однородной функцией первой степени. Для нее выполняется формула Эйлера

.

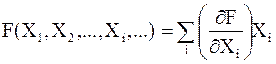Метод неопределенных множителей Лагранжа для нахождения экстремума функций нескольких переменных

Пусть кроме функции F=F(X₁,X₂,...,X_m+k), которую необходимо испытать на экстремум, имеются еще функции

Функции j_i называются функциями связи.

Для того, чтобы найти экстремум функции F, можно было бы, используя k уравнений связи, найти функцию от m независимых переменных. Однако при таком решении выкладки могут стать чрезвычайно сложными.

Лагранж предложил метод, по которому вводится вспомогательная функция

,

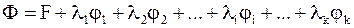в которую входят величины l₁,l₂,...,l_i,...,l_k, называемые неопределенными множителями.

Условию экстремума отвечают равенства

.

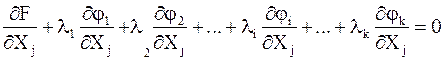j=1,2,...,m+k.

Задачи о размещении и расселении жильцов

Предлагаемые здесь задачи из комбинаторики являются иллюстрацией проблемы реализации системы.

Вначале рассмотрим более простую задачу о размещении.

Предположим, что имеется книжный шкаф, в который можно поставить n книг. Книги отличаются друг от друга (возможно, названием произведений, именем автора, номером тома и т.д.). Каждая последовательность расположения книг, отличающаяся от других, считается отдельной расстановкой (или размещением). Подсчитаем, сколько может быть таких размещений.

Пусть в шкафу имеется n мест для книг (полок, ящиков и т.п.).

Когда шкаф пуст, то первая размещаемая книга может занять любое из n возможных мест. Следовательно, для одной книги существует n способов размещения. Вторую книгу можно поставить на любое из n-1 оставшихся мест. Поэтому для двух книг существует n×(n-1) способов размещения. Третья книга ставится на любое из оставшихся (n-2) мест, и для размещения трех книг существуют n×(n-1)×(n-2) способов размещения... Перейдем к размещению одной из последних трех книг. До этого предыдущие книги можно было разместить

n×(n-1)×(n-2)×...×4 способами. Одна из оставшихся трех книг может быть размещена тремя способами и общее число размещений увеличится до

n×(n-1)×(n-2)×(n-3)×...×4×3. Предпоследнюю книгу можно разместить двумя способами, а последнюю - одним, и число размещений всех книг составит n×(n-1)×(n-2)×(n-3)×...×4×3×2×1= n!.

Теперь обратимся к более сложной задаче.

Пусть необходимо расселить N человек в m домах. В первом доме можно поселить N₁ жильцов, во втором - N₂, ..., в доме i - N_i,,... Если бы квартиры в каждом доме были различимы, то число расселений составило бы N!. Примем , что квартиры в каждом доме равноценны, т.е. переселение жильцов из квартиры в квартиру в пределах одного дома не учитывается. Таким образом, общее число возможных расселений N! должно быть уменьшено. Число исключенных способов заселения первого дома составит N₁!, второго - N₂!, ..., i-го - N_i!, ... и общее число расселений уменьшится в N₁!N₂!...N_i!...=PN_i! раз.

В таком случае все дома можно заселить следующим числом способов:

.

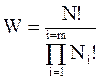Формула Стирлинга

Во многих задачах требуется переход от N! к непрерывной функции. В этом случае используют приближение, именуемое формулой Стирлинга:

.

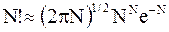Начиная с N=12, приближение становится исключительно хорошим. Для систем, содержащих молекулы (напомним, что постоянная Авогадро близка к 6×10²³), приближение является замечательным.