Диссипативная функция и потоки

Обозначим производство энтропии следующим образом:

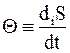
и введем новую функцию Y, определяемую следующим равенством:

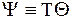. (12 - 3)

Функция Y называется диссипативной функцией.

Если внутренняя энергия не изменяется, то производство энтропии происходит в результате диссипации (рассеивания) работы и протекания химической реакции, приводящей к изменению чисел молей веществ

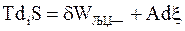, (12 - 4)

где А - сродство химической реакции,

x - химическая переменная,

dW - диссипируемая (рассеиваемая) работа.

Согласно выражению (12 - 3) из уравнения (12 - 4) следует

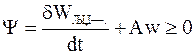, (12 - 5)

где 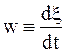- скорость химической реакции.

Классическим примером диссипативного явления может служить прохождение электрического тока через электропроводящую среду без химической или электрохимической реакции. В этом случае электрическая работа равна

,

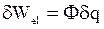где F - внешняя разность потенциалов, q - переносимый заряд.

Следовательно,

,

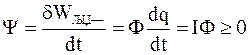где I - сила тока.

В общем случае диссипативная функция может быть представлена в виде суммы произведений величин J_i, называемых обобщенными потоками (в приведенном выше примере к обобщенным потокам относится сила тока), на величины X_i, называемые обобщенными силами ( в приведенном выше примере такой силой служит разность потенциалов):

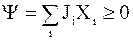. (12 - 6)

При равновесии становится равной нулю не только диссипативная функция, но и каждое произведение, так как оно является линейно независимым. Для реально протекающих процессов выполняется неравенство.