Примеры использования распределения Больцмана

Распределение частиц по высоте

Энергия частицы, находящейся на высоте h от отсчетного уровня в поле силы тяжести и имеющей массу m, плотность r_p, равна

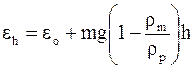, (11 - 27)

а на отсчетном уровне она равна e_о. В уравнение (11 - 27) входит также плотность среды r_m.

Пусть N_h обозначает число частиц на высоте h, а N_o - на отсчетном (нулевом) уровне.

Число частиц на каждом уровне можно определить по уравнению Больцмана (11 - 18). Разделив N_h на N_o, можно избавиться от суммы по состояниям

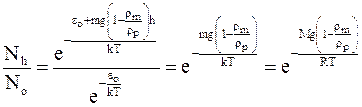^. (11 - 28)

Последняя часть уравнения (11 - 28) представлена в форме, содержащей молярную массу M=mN_A и универсальную газовую постоянную R=kN_A.

Совпадение уравнения (11 - 28) с уравнением (10 - 9), следующим из уравнений классической термодинамики, очевидно.

Уравнение (11 - 28) было использовано Перреном для экспериментального определения константы Больцмана и постоянной Авогадро.

Распределение заряженных частиц в электрическом поле

Энергия иона в электрическом поле равна

,

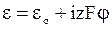где e_о - составляющая энергии, не зависящая от электрического поля,

i - знак заряда иона («+» для катиона и «-» для аниона),

z - заряд иона в атомных единицах заряда,

j- электрический потенциал в данной точке раствора.

Приняв , что электрический потенциал в точке, значительно отдаленной от заряженной поверхности, равен нулю, можно найти отношение числа частиц в этих точках. Так как это отношение прямо пропорционально отношению концентраций, то получаемое уравнение совпадет с уравнением (10 - 11).