Константа Больцмана. Методы ее определения. Среднее значение энергии частиц
Установить зависимость между константой Больцмана и другими фундаментальными постоянными можно, приравняв величину средней энергии молекул, найденную разными способами.
С этой целью рассмотрим одноатомный идеальный газ, заключенный в кубическую емкость с длиной ребра а.
Пусть молярная масса вещества равна М, а средняя скорость движения молекул газа при температуре Т равна u.
Энергия молекул определяется только кинетической составляющей, равной
,
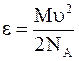где NA - постоянная Авогадро (отношение молярной массы к постоянной Авогадро представляет собой массу одной молекулы).
Найдем импульс, получаемый стенкой при нормальном ударе одной молекулы:
.
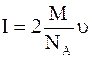Для того, чтобы определить число ударов молекул в единицу времени, необходимо учитывать, что движение молекул по каждому координатному направлению равновероятно. Поэтому принимается, что 1/3 молекул движется от одной стенки куба к противоположной и обратно.
Количество вещества n, содержащегося в кубической емкости с объемом а3, найдем по уравнению состояния идеального газа
,
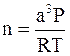а число молекул составляет
.
Как уже указывалось, 1/3 из этого числа движется в заданном направлении, причем каждая молекула совершает в единицу времени число пробегов от стенки и обратно, которое определяется равенством
.
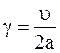Следовательно, число ударов всех молекул в единицу времени равно
,
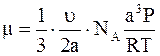а сила ударов по стенке составляет
.
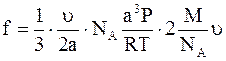Давление газа равно
.
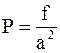Отсюда 
и средняя энергия одноатомной молекулы составляет
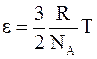. (11 - 19)
Теперь найдем среднюю энергию молекулы, используя распределение Больцмана. Для этого несколько преобразуем формулу Больцмана.
Вновь обратимся к постулату о равноценности движения по всем направлениям и будем исходить из следующего условия.
Пусть для некоторой части молекул одноатомного газа импульсы находятся в пределах от Px до Px+dPx, от Py до Py+dPy и от Pz до Pz+dPz.
Согласно распределению Больцмана доля этих молекул в общем числе молекул прямо пропорциональна фактору Больцмана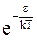 
. Кроме того, она должна быть прямо пропорциональна выделенному объему поля импульсов dPxdPydPz. Принимая, что число молекул dN с энергией e и заданным объемом поля импульсов dPxdPydPz является очень малой величиной, распределению Больцмана можно придать следующий вид:
. (11 - 20)
В уравнении (11 - 20) s - коэффициент пропорциональности. Для его определения воспользуемся тем, что общее число молекул в системе является постоянной величиной: N=const. Интегрирование уравнения (11 - 20) дает
.
Следовательно,
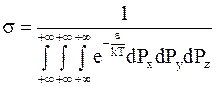
и распределение молекул одноатомного газа принимает вид:
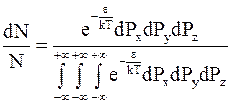. (11 - 21)
Уравнение (11 - 21) можно дальше преобразовывать, переходя к полярным координатам.
Элемент объема шарового слоя в полярных координатах равен
.
Зависимость между энергией и импульсами можно представить следующим образом:
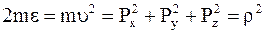
или
,
из чего следует для частиц постоянной массы m
.
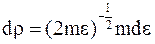Заменим элемент объема поля импульсов на величину, определяемую только энергией молекул:
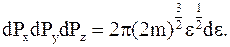
Переход от поля импульсов к распределению по энергии приводит к изменению пределов интегрирования. Скорость молекул может быть положительной и отрицательной, и пределы интегрирования по импульсам могут быть от +¥ до -¥. Энергия может иметь минимальное значение, равное 0 и максимальное - условно равное ¥.
С учетом изложенного получаем
.
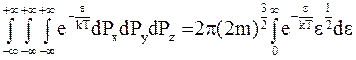Интеграл в приведенном выше уравнении является табличным интегралом следующего типа:
,
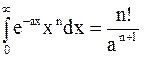где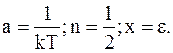 
Кроме того, 
.
Таким образом, уравнение Больцмана для распределения молекул по энергиям в непрерывном спектре можно записать в следующем виде:
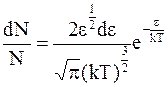. (11 - 22)
Среднее значение какой-либо величины 
при непрерывном распределении частиц представляет собой деленный на общее число частиц интеграл произведения этой величины на число молекул, обладающих ее значением Х:
.
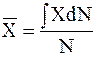Среднее значение энергии молекул одноатомного газа определяется по уравнению
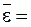
(11 - 23)
или с учетом уравнения (11 - 22)
.
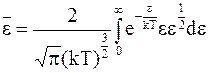Обращаясь вновь к табличному интегралу, найдем
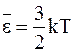. (11 - 24)
Сравнивая (11 - 19) и (11 - 24), имеем
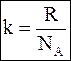. (11 - 25)
Молекулы одноатомного идеального газа участвуют только в поступательном движении по трем координатным направлениям. Число направлений движения называется также числом степеней свободы .
В предположении равноценности движения по каждому направлению уравнения (11 - 19) и (11 - 24) позволяют сделать важный вывод:
В идеальном газе на каждую степень свободы приходится энергия, равная 1/2kT.
Многоатомные молекулы кроме поступательного участвуют во вращательном движении. В частности, для двухатомных молекул существуют еще две степени вращательного движения.
Следовательно, энергия молекул двухатомного идеального газа равна 5/2kT.
Внутренняя энергия идеального газа определяется только кинетической составляющей молекул. Для одного моля частиц
.
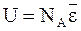В связи с этим производные внутренней энергии по температуре при постоянном объеме таковы:
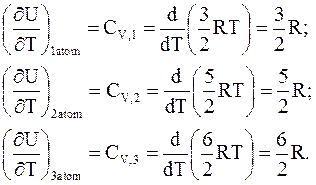(11 - 26)
Уравнения (11 - 26) объясняют природу теплоемкости идеального газа.
Дата добавления: 2015-07-24; просмотров: 1075;