Распределение Больцмана. Обратимся к системе с дискретным спектром значений энергии молекул: e1,e2,e3, ,ei ,

Обратимся к системе с дискретным спектром значений энергии молекул: e₁,e₂,e₃, ...,e_i , ...

Если этими значениями энергии обладают молекулы, числа которых соответственно равны N₁, N₂, N₃, ..., Ni,..., то общее число частиц в системе равно

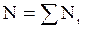, (11 - 8)

а полная энергия системы равна

. (11 - 9)

Энтропию системы найдем по формуле Больцмана

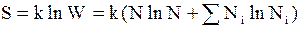. (11 - 10)

Для изолированной системы условием равновесия является максимум энтропии. Поэтому для нахождения распределения числа частиц по энергиям необходимо найти условие этого максимума. Простое дифференцирование функции S по числу частиц в данном случае непригодно, так как кроме основного уравнения (11 - 10) имеются дополнительные уравнения с теми же независимыми величинами - уравнения связи - (11 - 8) и (11 - 9). В этих условиях для нахождения экстремума используется метод неопределенных множителей Лагранжа. В соответствии с этим методом составляется функция

или

,.

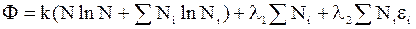где l₁ и l₂ - неопределенные множители Лагранжа.

Дифференцирование функции Ф с учетом

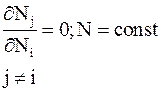
позволяет найти условие максимума энтропии:

. (11 - 11)

Преобразуем уравнение (11 - 11)

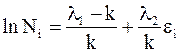
и введем новые обозначения для входящих в него констант:

.

Их применение упрощает форму записи уравнения (11 - 11)

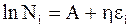. (11 - 12)

Потенцирование уравнения (11 - 12) дает

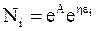
или, обозначив 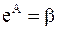, получим

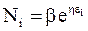. (11 - 13)

От константы b можно избавиться следующим образом.

Суммируя N_i, получим

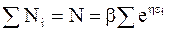. (11 - 14)

Деление (11-13) на (11-14) дает

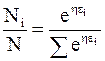. (11 - 15)

Уравнение (11 - 15) связывает число молекул (или других частиц) со значениями их энергии в системе. Таким образом, поставленная задача могла бы считаться решенной, если бы был ясен смысл входящей в уравнение (11-15) величины h. Чтобы установить его, прологарифмируем уравнение (11 - 15)

,

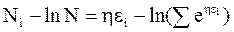умножим обе части уравнения на N_i

и просуммируем

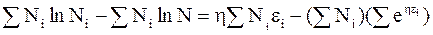
или

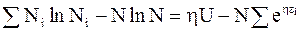. (11 - 16)

Обращаясь к уравнению (11 - 10), можно заметить, что левая часть равенства (11 - 16) равна 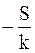. Следовательно,

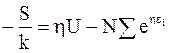. (11 - 16а)

При заданном энергетическом спектре системы, т.е. наборе значений энергии, и заданном числе частиц в системе последний член правой части равенства (11 - 16) является константой.

Исходя из изложенного, найдем приращения левой и правой частей равенства (11 - 16)

.

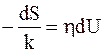Из второго постулата термодинамики для системы, находящейся при постоянном объеме и не совершающей полезную работу, следует

.

Сравнение двух последних уравнений дает

. (11 - 17)

С учетом соотношения (11 - 17) уравнение, описывающее распределение частиц по энергиям, принимает следующий вид:

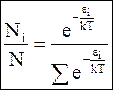(11 - 18)

Уравнение (11 - 18) называется уравнением Больцмана .

Входящая в уравнение (11 - 18) константа k называется константой Больцмана. Экспонента , определяющая относительное число частиц с данной энергией, называется фактором Больцмана . Сумма экспонент, входящая в знаменатель правой части уравнения (11 - 18), называется суммой по состояниям . Очень часто она обозначается f.