Частные случаи равновесия в непрерывных системах

Барометрическое уравнение

Барометрическое уравнение устанавливает зависимость давления газа по высоте. Существуют восходящие еще к Лапласу многочисленные методы вывода этого уравнения. В данном случае воспользуемся тем, что газ, находящийся в поле силы тяжести, является непрерывной системой, содержащей один компонент - газ с молярной массой М.

Химический потенциал газа зависит от его парциального давления, которое в данном примере совпадает с общим давлением на высоте h:

;

.

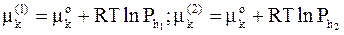Величины, определяющие потенциал и фактор количества вещества, рассматривались в п.1. Их подстановка в уравнение (10 - 7) дает

.

После преобразований получим

. (10 - 8)

Уравнение (10 - 8) называется барометрическим уравнением .

Распределение концентрации по высоте

В достаточно разбавленном растворе химический потенциал можно выразить через молярную концентрацию

.

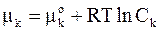Если растворяемое вещество имеет плотность r_2,, а растворитель - плотность r₁, то потенциал в заданной точке выражается с учетом архимедовой поправки

.

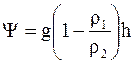Подстановка соответствующих величин в уравнение (10 - 7) дает

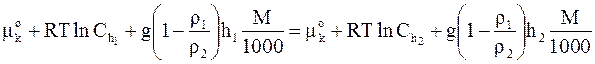
После преобразований получим

. (10 - 9)

Расчеты по уравнению (10 - 9) показывают, что для обычных молекул концентрация с высотой изменяется настолько слабо, что эти изменения экспериментально определить невозможно. Однако для коллоидных частиц, содержащих порядка тысяч первичных молекул, концентрация резко изменяется с высотой.

Для достижения заметного изменения концентрации макромолекул с высотой силу тяжести заменяют центробежной силой.

Равновесие в электрическом поле

При переносе одного моля ионов с атомным зарядом (+1) из точки с электрическим потенциалом j₁ в точку с потенциалом j₂ фактор количества вещества оказывается равным числу Фарадея F. Если переносится 1 моль ионов с зарядом z, то фактор количества составит zF. С учетом изложенного в системе (при отсутствии ассоциации частиц) в качестве условия равновесия можно принять

. (10 - 10)

Величина m_ech, определяемая равенством (10 - 10), называется электрохимическим потенциалом .

Электрохимический потенциал играет важную роль в электрохимии, особенно при построении модели двойного электрического слоя.

Определим концентрацию катионов, заряд которых в атомных единицах равен z₊, и анионов с зарядом z_- в точке с электрическим потенциалом j вблизи заряженной поверхности.

Для простоты примем зависимость химических потенциалов от концентраций ионов в форме

.

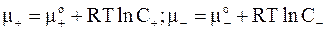В этом случае электрохимические потенциалы ионов окажутся равными

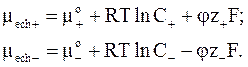
В объеме раствора (на относительно большом расстоянии от поверхности) электрический потенциал можно принять равным нулю. Если концентрации ионов в объеме равны 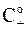и , то электрохимические равновесия можно описать уравнениями

или

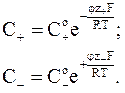(10 - 11)

Алгебраическая сумма произведений концентраций ионов на их заряд равна плотности заряда в данной точке.

Более детально распределение заряженных частиц вблизи заряженной поверхности рассматривается в курсе коллоидной химии.