Термодинамическая вероятность

Вообразим следующий эксперимент, реальное проведение которого невозможно.

В системе (возможно, ею окажется идеальный газ) каким-то образом пометим и сфотографируем все молекулы с таким расчетом, чтобы можно было определить их энергию. Результаты такого эксперимента представим в виде таблицы, в которой приводятся все возможные значения энергии молекул в системе и число молекул с каждым значением энергии.

Таблица 11 - 1.

Условное распределение молекул по энергиям

Если молекулы помечены, т.е. различимы, то появляется возможность подсчитать число способов распределения молекул по значениям энергии наподобие того, как рассчитывается размещение жильцов по домам (см. приложение). Для этого воспользуемся формулой

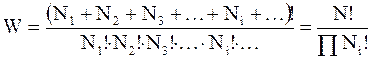. (11 - 1)

Число способов распределения молекул по энергиям W называется также числом способов реализации данной системы или (что наиболее распространено) термодинамической вероятностью .

Отметим, что термодинамическую вероятность с математической вероятностью объединяет название и единственное свойство, с которым познакомимся при дальнейшем рассмотрении этого понятия. Различия между ними весьма существенны. Минимальное значение математической вероятности равно 0 (невозможное событие), а максимальное равно 1 (абсолютно достоверное событие). Минимальное значение термодинамической вероятности составляет 1 (молекулы могут быть распределены по энергиям единственным способом). Верхнего предела для термодинамической вероятности нет.

Если бы значения чисел были невелики, то для расчетов термодинамической вероятности можно было воспользоваться уравнением (11 - 1) в исходной форме. Для больших чисел, а именно с ними приходится сталкиваться, оперируя с числом молекул в системе, применяется замечательное приближение

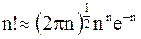, (11 - 2)

называемое формулой Стирлинга .

Можно воспользоваться более грубым, но достаточным для наших целей приближением, учитывающим, что для больших чисел n>>2p и ln n<<n,

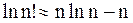. (11 - 3)

Расчетная формула для термодинамической вероятности системы с реальным числом частиц принимает следующий вид:

.

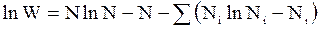Так как SN_i=N, то формула становится еще проще:

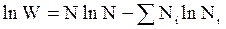. (11 - 4)

Найдем термодинамическую вероятность системы, образованной сложением равновесных подсистем, одна из которых содержит aN частиц, а другая содержит bN частиц. Относительное распределение частиц по энергиям в равновесных системах совпадает. Поэтому расчет термодинамической вероятности по составной формуле (11 - 4) приводит к следующему:

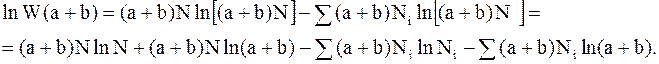
Принимая во внимание, что число подсистем значительно меньше числа частиц в каждой из них, т.е. a+ b<<N_i, получим

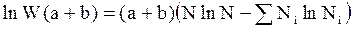
или

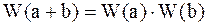, (11 - 5)

так как .

Формула (11 - 5) показывает, что термодинамическая вероятность системы, полученной сложением подсистем, равна произведению термодинамических вероятностей подсистем. Это свойство термодинамической вероятности называется мультипликативностью .

Мультипликативность характерна и для математической вероятности. Как известно, математическая вероятность исхода нескольких независимых событий равна произведению вероятностей исхода каждого из них.