Вероятность нахождения в работоспособном состоянии

Для фиксированного момента времени t_i вероятность того, что объект работоспособен, равна

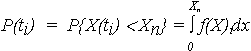
(1)

где f(X)_i - плотность распределения значений ОП при t = t_i , т.е. в i- м сечении случайного процесса Х(t).

В частном случае при нормальном распределении ОП вероятность P(t_i) определяется

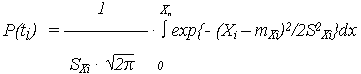
(2)

где m_xi , S_xi - указанные ранее параметры (числовые характеристики) распределения случайного ОП Х_i = {X}_i .

Переходя к случайной величине

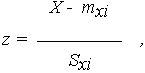
(3)

имеющей нормальное распределение с параметрами, соответственно, МО и СКО M{Z} = 0, S{Z} = 1 и плотностью распределения

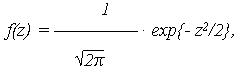
(4)

выражение (2) можно записать через функцию Лапласа Ф(z)

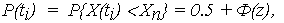
(5)

где Ф(z) определяется по выражению

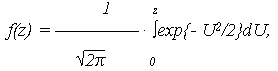
(6)

и является табулированной.

15.1.2. Плотность распределения наработки до отказа

При случайном процессе изменения ОП, имеющем монотонные реализации, плотность распределения времени выхода ОП за границу X_п рабочей области (плотность распределения времени до отказа) для момента t_i равна

 

f (ti) = - dP(t)/dt|t=ti = dQ(t)/dt|t=ti

(7)

где Q(t_i) - вероятность нахождения объекта в неработоспособном состоянии, определяемая через известную по (1) P(t_i)

Q(ti) = P{X(ti) Xп} = 1 - P(ti).

(8)

С учетом выражений (1) и (8) вероятность нахождения объекта в неработоспособном состоянии

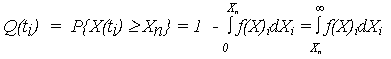
(9)

а с учетом функции Лапласа Ф(z) при нормальном распределении ОП в t_i, 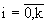сечениях

Q(ti) = 0.5 - Ф(z).

(10)