Сравнительные характеристики программных и аппаратурных отказов.

Программные отказы изделия и аппаратурные отказы имеют много общего, но во многом существенно различаются. Общее между ними:

а) невыполнение объектом заданных функций;

б) времена до отказов и времена устранения отказов носят случайный характер;

в) методы обработки статистических данных об отказах одинаковы, а потому статистические оценки показателей надёжности аппаратурной и программной, полученные по результатам испытаний и эксплуатации, могут быть одинаковыми по своему названию: средняя наработка объекта на программный отказ, интенсивность программных отказов объекта и т.д. Возможны и объединённые (комплексные) оценки: средняя наработка объекта на программный и аппаратурный отказ и т.п.

Вместе с тем отказы программные существенно отличаются от отказов аппаратурных:

а) отказ аппаратурный зависит либо от времени, либо от объёма выполненной работы, а отказ программный - от той функции, которую выполняет изделие под управлением программы (точнее, от того, с какой вероятностью программа выйдет на такой участок, который содержит ошибку);

б) обнаружение и устранение аппаратурного отказа (заменой отказавшего элемента исправным) не означает, что такой же отказ не повторится при дальнейшей работе изделия, а обнаружение и устранение отказа программного (исправление программы) означает, что такой отказ в дальнейшем не повторится;

в) программный отказ, обнаруживаемый при автономной проверке программы, может переходить в разряд недействующих, если состояние аппаратуры делает её нечувствительной к данному виду программного отказа. Например, если в программе ошибочно не предусмотрена программная защита от аппаратурного сбоя, то это программный отказ, но если при этом в аппаратуре не возникает сбоя, то отказ программный становится недействующим;

г) прогнозировать возникновение аппаратурных отказов сравнительно легко, а прогнозировать возникновение отдельных программных отказов трудно, а часто и невозможно. Для отдельных программных отказов трудно предвидеть время, когда они становятся действующими, а когда - недействующими;

д) аппаратурные отказы целесообразно подразделять на внезапные и постепенные, т.е. отказы, различные по своей физической природе, законам распределения времени до отказа, методам борьбы за снижение их вероятности. Программные отказы нет смысла делить на внезапные и постепенные. Они возникают внезапно, как только программа переходит на такой участок, который содержит “ошибку”. В то же время они по природе своей не совпадают с внезапными аппаратурными отказами. Вероятность их возникновения не связана с продолжительностью работы изделия, а связана с условной вероятностью того, что программа содержит ошибку в данной части программы, и вероятностью того, что изделие будет работать под управлением этой части программы.

16.2 Проверка и испытания программ.

Испытания программ на надёжность и испытания изделий на надёжность их программного обеспечения - обязательные этапы при проверке надёжности систем.

Испытания с целью проверки надёжности программ осуществляются с помощью специальных программ (тестирование) и специальных (имитационных) стендов. Проверяется при этом степень отработанности программы и её соответствие заданным требованиям.

Испытания с целью проверки надёжности изделий, работающих под управлением программ, осуществляются при совместной работе программы и изделия. Проверяются при этом и степень отработанности программы в соответствии с заданными требованиями, и корректность этих требований, и согласованность взаимодействий программы и аппаратуры.

Степень отработанности программы может проверяться различными методами. Чем выше требование к достоверности проверки, тем более сложен метод проверки.

Рассмотрим один из наиболее простых методов. В процессе проверки “корректности” программы (с помощью наблюдений за работой либо изделия, либо имитирующего устройства, либо на специальном стенде с помощью тестов) фиксируются времена обнаружения ошибок в программе. Результаты проверки обрабатываются при следующих предположениях: 1) ошибки программы независимы. Каждый раз после обнаружения они устраняются и в дальнейшем не проявляются. 2) интенсивность ошибок уменьшается по мере их обнаружения и устранения.

Статистическая интенсивность программных l ошибок определяется так же как интенсивность аппаратных отказов по формуле:

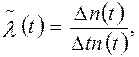
где n(t) - число идентичных программ, не отказавших к моменту времени t; Dn(t) - число отказавших идентичных программ на интервале (t, t + Dt).

Выявление и устранение ошибок производится до тех пор, пока значение 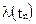будет меньше заданного значения. Заданное значение 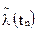назначается с учётом требований к надёжности изделия. Ориентировочно можно исходить из того, что интенсивность программных ошибок, приводящих к отказу, на этапе отладочных испытаний должна быть не больше интенсивности аппаратурных отказов.

Положение о том, что при создании программного обеспечения больших систем возможно возникновение ошибок и что выявление программных ошибок - чрезвычайно трудная задача, не только не должно обезоруживать разработчиков систем, а наоборот, должно ориентировать их на максимальное сосредоточение сил для ликвидации программных отказов.

Влияние программных ошибок на надёжность изделия должно непрерывно уменьшаться с каждым новым этапом освоения программ (разработка - отладка - опытная эксплуатация - нормальная эксплуатация) так, чтобы на этапе нормальной эксплуатации объекта программная надёжность его была на уровне заданных требований.

16.3 Основные проблемы исследования надёжности программного обеспечения.

В сложной программно - управляемой технической системе любого типа можно выделить две основные, относительно независимые части.

1. Совокупность автономно, параллельно работающих технических схем и устройств - аппаратная часть.

Совокупность программ, ориентированных на решение данного комплекса задач, представляющих математическое обеспечение технической системы и образующих её программную часть (операционная система и рабочие программы пользователей).

При общем анализе характеристик технической системы (её надёжности) следует учитывать, что если аппаратная часть жестко задана, неизменна и её надёжность может быть обеспечена на требуемом уровне, то программная часть в каждом отдельном случае может иметь ряд модификаций, является достаточно гибкой, изменяемой частью технической системы и в обеспечении совокупной надёжности системы определяет наибольшее количество ошибок. Авторы [19] считают, что в настоящее время около половины отказов сложных вычислительных систем обусловлено ошибками программ, а с ростом надёжности элементной базы (ИС, БИС) число отказов, связанных с математическим обеспечением, возрастает до 90% от общего числа отказов.

К основным проблемам исследования надёжности программного обеспечения (ПО) относится:

Разработка методов оценки и прогнозирования надёжности ПО на основе совокупности количественных показателей и характеристик, идентичных показателям аппаратурной надёжности.

Определение факторов, влияющих на достижение заданного уровня надёжности ПО.

Разработка методов, обеспечивающих достижение заданного уровня надёжности ПО.

Совершенствование методов повышения надёжности ПО в процессе проектирования и эксплуатации.

Эффективный способ повышения надёжности ПО - использование методов структурного проектирования программ, так как в зависимости от структуры ПО последствия отдельных ошибок могут быть легко обнаружены, локализованы и исправлены на некотором небольшом участке программы либо распространиться на другие уровни и модули ПО.

16.4 Критерии оценки надёжности программных изделий.

Всё множество различных показателей надёжности программных систем можно разбить на две большие группы:

Количественные показатели надёжности ПО.

Качественные показатели надёжности ПО.

Не рассматривая качественные характеристики надёжности, которые достаточно подробно исследованы в [20, 21], остановимся более подробно на возможности использования количественных показателей для оценки и прогнозирования надёжности ПО.

Наиболее удобно в качестве таких показателей использовать статистические (вероятностные) критерии хорошо разработанной теории надёжности радиоэлектронной аппаратуры. Следует учитывать, что оценка надёжности ПО на основе статистической теории надёжности аппаратуры возможна в пределах некоторых ограничений, учитывающих специфику ПО как определённого вида продукта человеческого труда.

Можно выделить следующие характеристики и количественные показатели надёжности ПО:

Безотказность. Говоря о безотказности ПО, характеризующей способность ПО выполнять заданные функции в заданных условиях эксплуатации технической системы, будем считать, что отказ программы - это результат проявления скрытой ошибки. Следует иметь в виду, что входные данные и данные создаваемые программой, не являются элементами ПО, поскольку их надёжность связана с работой внешних устройств и аппаратной части системы. Только константы, вводимые программистом, считаются частью ПО.

Для невосстанавливаемых в ходе эксплуатации программ обобщённой характеристикой надёжности (безотказности) является вероятность безотказной работы P(t), характеризующая вероятность того, что за время t отказа не произойдёт:

P(t) = P(T ³ t) = 1 - q(t);

где T - время работы ПО до отказа или наработка ПО до отказа (T - случайная величина); q(t) - вероятность отказа ПО.

Отсюда можно определить функцию интенсивности отказов:

;

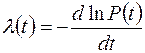Среднее время наработки до наступления отказа (среднее время безотказной работы) определяется как математическое ожидание временного интервала между двумя последовательными нарушениями работоспособности ПО:

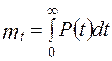
Для экспоненциального закона распределения отказов:

;

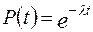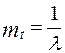
Поскольку программы имеют явно выраженные производственные циклы работы, то наработка программы может быть выражена либо через календарное время, либо через машинное время, либо через количество отработанных операторов, решённых задач и т.п.

Один из способов оценки 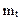- наблюдение за поведением программы в определённый временной период. Тогда величину среднего времени между отказами (сбоями) ПО можно определить так:

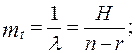
где H - общее количество часов успешного прогона программы, определяемое по формуле:

;

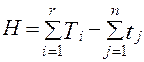где - время непрерывного прогона в часах безошибочной работы ПО;

n - общее количество прогонов ПО; r - количество прогонов ПО без ошибок; l = n -r - количество прогонов с ошибками; 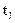- время прогона в часах до проявления ошибки ПО.

Полагая количество ошибок постоянным, можно вычислить интенсивность отказов ПО, приведённую к одному часу работы 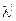, и среднее время между соседними отказами ПО.

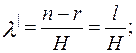
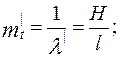
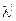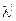Классифицируя отказы ПО по видам отказов - аппаратные, программные, оператора и т.д., можно определить частные (взвешенные) интенсивности отказов по соответствующим видам ошибок - ап, пр, 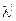оп и т.д., а общая надёжность определяется как сумма таких интенсивностей. Такой подход может значительно облегчить сбор статистических данных по соответствующим видам отказов на основе независимого анализа программных изделий различных типов.

В случае, если в ходе эксплуатации возможна корректировка ПО или восстановление программы после отказа, вызванного действием помех (сбоев) от внепрограммных источников, а время восстановления достаточно мало по сравнению с временем между отказами или сбоями, обобщающей характеристикой безотказности ПО является интенсивность потока отказов во времени .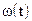

;

;

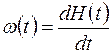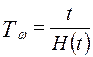где H(t) - среднее число отказов за время t; 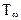- среднее время наработки между двумя отказами.

Для программ, время корректировки которых сравнимо с временем между отказами, обобщающей характеристикой безотказности является функция коэффициента готовности 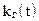в зависимости от времени. Показатель готовности характеризует вероятность застать систему в заданный момент времени в работоспособном состоянии.

2. Устойчивость. Устойчивость ПО определяет способность системы выполнять заданные функции в условиях действия помех (ошибок, сбоев, отказов), возникающих во внепрограммных источниках (техническое обеспечение, исходные данные). При оценке устойчивости ПО должны быть заданы параметры окружающей среды, по отношению к которой оценивается устойчивость программ.

Показатели устойчивости - это показатели безотказности, но с использованием условных вероятностей. Условием, при котором вычисляются вероятности, является отказ (сбой) в программе или аппаратуре.

Для невосстанавливаемых (некорректируемых) программ обобщённым показателем устойчивости служит условная вероятность безотказной работы:

где P(A) - вероятность ошибки (сбоя) программы или отказа аппаратуры.

Безотказность и устойчивость - динамические характеристики, то есть они характеризуют надёжность ПО в процессе работы.

3. Корректируемость. Этот показатель надёжности ПО аналогичен показателю ремонтопригодности радиоэлектронной аппаратуры, характеризует приспособленность ПО к поиску и устранению ошибок и внесению в него изменений в ходе эксплуатации. Он используется для характеристики восстанавливаемых в ходе эксплуатации программ. Показатели корректируемости: время корректировки 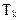, вероятность корректировки программы за заданное время 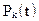, коэффициент готовности 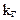, параметр потока корректировок .

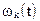4. Защищённость и долговечность. Дополнительными характеристиками надёжности ПО являются: показатель защищённости от посторонних вмешательств в работу ПО и показатель долговечности, характеризующий свойства программ избегать морального старения при длительном использовании. Защищённость характеризуется вероятностью внесения искажений при постороннем вмешательстве, а долговечность - временем отказа ПО вследствие морального старения.

В зависимости от условий применения ПО можно выделить три режима (типа) его работы:

Программа не корректируется, и любой отказ является полным, т.е. после отказа ПО не восстанавливается. Основные показатели надёжности для этого режима работы программ - безотказность, устойчивость и защищённость.

Программа не корректируется, однако после отказа ПО система продолжает функционировать нормально. Основные показатели надёжности - безотказность, устойчивость, защищённость и долговечность.

После каждого отказа ПО корректируется, отлаживается и только после этого снова сдаётся в эксплуатацию. Основные показатели надёжности - безотказность, устойчивость, корректируемость, защищённость, а также потери времени.

16.5 Критерии надёжности сложных комплексов программ.

Для оценки надёжности программ, как и при исследовании характеристик аппаратуры, как правило, приходится ограничиваться интегральными показателями наработки на отказ и средним временем восстановления. Определение остальных показателей сопряжено с большими трудностями, которые обусловлены тем, что для определения показателей надёжности комплексов программ необходимы длительные эксперименты или сложные расчёты при определённых исходных данных.

Оценка достоверности результатов и надёжности функционирования комплекса программ представляет собой сложную задачу из-за “проклятия размерности”. Естественным становится статистический подход к анализу надёжности функционирования и статистическая оценка достоверности результатов. Качество отладки определяется интенсивностью (частотой) отказов и значениями ошибок в выходных результатах, полученными за счёт не выявленных ошибок в программах и искажений исходных данных. Интенсивность (частота) отказов в комплексе программ иначе называется как частота проявления ошибок в комплексе программ.

Точное определение полного количества ошибок в программе прямыми методами измерения невозможно. Имеются только косвенные пути статистической оценки их полного количества. Такие оценки базируются на построении математических моделей в предположении жёсткой корреляции между общим количеством и проявлениями ошибок в комплексе программ после его отладки в течении времени t, т.е. между следующими параметрами:

суммарным количеством ошибок 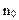в комплексе программ,

количеством ошибок, выявляемых в единицу времени dn/dt в процессе тестирования и отладки при постоянных усилиях на их проведение;

интенсивностью отказов l или числом искажений результатов на выходе комплекса программ вследствие не выявленных ошибок при нормальном функционировании системы в единицу времени.

На рис.3.2 показаны зависимости 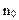, dn/dt и l от времени отладки (масштабы по оси ординат не совпадают)

l

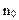
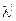
t

dn/dt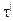

Рис. 3.2

16.6 Математические модели надёжности комплексов программ.

Математические модели позволяют оценивать характеристики ошибок в программах и прогнозировать их надёжность при проектировании и эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:

- показателей надёжности комплексов программ в процессе отладки;

- количества ошибок, оставшихся не выявленными;

- времени, необходимого для обнаружения следующей ошибки в функционирующей программе;

- времени, необходимого для выявления всех ошибок с заданной вероятностью.

Использование моделей позволяет эффективно и целеустремлённо проводить отладку и испытания комплексов программ, помогает принять рациональное решение о времени прекращения отладочных работ.

В настоящее время предложен ряд математических моделей, основными из которых являются:

- экспоненциальная модель изменения ошибок в зависимости от времени отладки;

- модель, учитывающая дискретно - понижающуюся частоту появления ошибок как линейную функцию времени тестирования и испытаний;

- модель, базирующаяся на распределении Вейбула;

- модель, основанная на дискретном гипергеометрическом распределении.

При обосновании математических моделей выдвигаются некоторые гипотезы о характере проявления ошибок в комплексе программ. Наиболее обоснованными представляются предположения, на которых базируется первая экспоненциальная модель изменения ошибок в процессе отладки и которые заключаются в следующем:

1. Любые ошибки в программе являются независимыми и проявляются в случайные моменты времени.

2. Время работы между ошибками определяется средним временем выполнения команды на данной ЭВМ и средним числом команд, исполняемым между ошибками. Это означает, что интенсивность проявления ошибок при реальном функционировании программы зависит от среднего быстродействия ЭВМ.

3. Выбор отладочных тестов должен быть представительным и случайным, с тем чтобы исключить концентрацию необнаруженных ошибок для некоторых реальных условий функционирования программы.

4. Ошибка, являющаяся причиной искажения результатов, фиксируется и исправляется после завершения тестирования либо вообще не обнаруживается.

Из этих свойств следует, что при нормальных условиях эксплуатации количество ошибок, проявляющихся в некотором интервале времени, распределено по закону Пуассона. В результате длительность непрерывной работы между искажениями распределена экспоненциально.

Предположим, что в начале отладки комплекса программ при t = 0 в нём содержалось 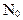ошибок. После отладки в течении времени t осталось 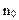ошибок и устранено n ошибок ( 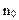+ n = 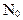). При этом время t соответствует длительности исполнения программ на вычислительной системе (ВС) для обнаружения ошибок и не учитывает простои машины, необходимые для анализа результатов и проведения корректировок.

Интенсивность обнаружения ошибок в программе dn/dt и абсолютное количество устранённых ошибок связываются уравнением

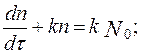где k - коэффициент.

Если предположить, что в начале отладки при t = 0 отсутствуют обнаруженные ошибки, то решение уравнения имеет вид

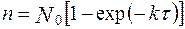
Количество оставшихся ошибок в комплексе программ

пропорционально интенсивности обнаружения dn/dt с точностью до коэффициента k.

Время безотказной работы программ до отказа T или наработка на отказ, который рассматривается как обнаруживаемое искажение программ, данных или вычислительного процесса, нарушающее работоспособность, равно величине, обратной интенсивности обнаружения отказов (ошибок):

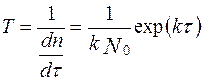
Если учесть, что до начала тестирования в комплексе программ содержалось 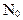ошибок и этому соответствовала наработка на отказ 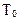, то функцию наработки на отказ от длительности проверок можно представить в следующем виде:

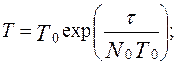
Если известны моменты обнаружения ошибок 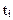и каждый раз в эти моменты обнаруживается и достоверно устраняется одна ошибка, то, используя метод максимального правдоподобия, можно получить уравнение для определения значения начального числа ошибок :

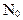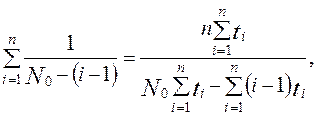
а также выражение для расчёта коэффициента пропорциональности

;

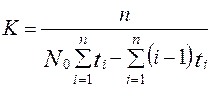В результате можно рассчитать число оставшихся в программе ошибок и среднюю наработку на отказ Tср = 1/l , т.е. получить оценку времени до обнаружения следующей ошибки.

В процессе отладки и испытаний программ, для повышения наработки на отказ от 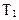до 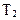, необходимо обнаружить и устранить Dn ошибок. Величина Dn определяется соотношением:

;

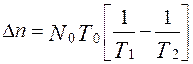Выражение для определения затрат времени Dt на проведение отладки, которые позволяют устранить Dn ошибок и соответственно повысить наработку на отказ от значения 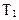до 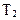, имеет вид:

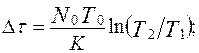
Вторая модель построена на основе гипотезы о том, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытания 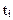между моментами обнаружения последовательных i - й и (i - 1) - й ошибок.

,

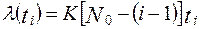где 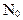- начальное количество ошибок; K - коэффициент пропорциональности, обеспечивающий равенство единице площади под кривой вероятности обнаружения ошибок.

Для оценки наработки на отказ получается выражение, соответствующее распределению Релея:

где .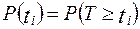

Отсюда плотность распределения времени наработки на отказ

.

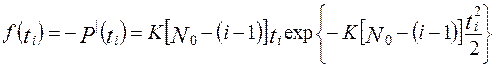Использовав функцию максимального правдоподобия, получим оценку для общего количества ошибок 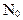и коэффициента K.

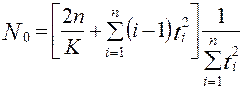
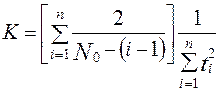
Особенностью третьей модели является учёт ступенчатого характера изменения надёжности при устранении очередной ошибки. В качестве основной функции рассматривается распределение времени наработки на отказ P(t). Если ошибки не устраняются, то интенсивность отказов является постоянной, что приводит к экспоненциальной модели для распределения:

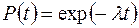
Отсюда плотность распределения наработки на отказ T определяется выражением:

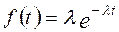
где t > 0, l > 0 и 1/l - среднее время наработки на отказ, т.е. Тср=1/l. Здесь Тср - среднее время наработки на отказ.

Для аппроксимации изменения интенсивности от времени при обнаружении и устранении ошибок используется функция следующего вида:

;

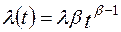Если 0 < b < 1, то интенсивность отказов снижается по мере отладки или в процессе эксплуатации. При таком виде функции l(t) плотность функции распределения наработки на отказ описывается двухпараметрическим распределением Вейбулла:

.

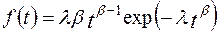Распределение Вейбулла достаточно хорошо отражает реальные зависимости при расчёте функции наработки на отказ.