Предварительная теорема Карно
Формулировка предварительной теоремы Карно:
Из всех циклических процессов, совершаемых квазистатически в данном температурном интервале, максимальным термодинамическим КПД обладает цикл Карно.
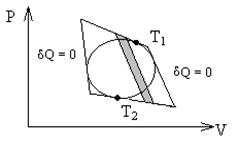Рис. 3 - 3. Произвольный цикл и описанный вокруг него цикл Карно в тех же температурных пределах.
|
Для доказательства возьмем произвольный цикл, как это показано на рис. 3 - 3.
Рис. 3 - 4. Сравнение фрагментов произвольного цикла и внутреннего цикла Карно.
|
Чтобы найти температурные пределы этого цикла, проведем изотермы. Верхняя изотерма, касающаяся цикла, соответствует его максимальной температуре (обозначим ее Т1), а нижняя изотерма, также касающаяся цикла, - нижней минимальной температуре (примем ее равной Т2). Далее проведем две адиабаты, касающиеся произвольного цикла. Заключенный между касательными изотермами и касательными адиабатами цикл является циклом Карно, проводимым в тех же температурных пределах, что и произвольный цикл.
Проведя произвольно на очень малом расстоянии друг от друга две адиабаты, выделим фрагменты произвольного цикла и цикла Карно (рис. 3 - 4). КПД фрагмента цикла Карно, описанного вокруг произвольного цикла, совпадает с КПД всего внешнего цикла Карно.
Площадь, ограниченная верхним и нижним фрагментами произвольного цикла и двумя боковыми адиабатами, равна сумме теплот dQ и dQ¯. Теплота dQ соответствует верхнему участку, а dQ¯ - нижнему. Сохраняя площадь выделенной части неизменной, проведем вместо верхнего фрагмента произвольного цикла изотерму. Обозначим ее температуру T1`. Теплота процесса остается прежней: dQ+dQ¯. Так как теплота нижней части фрагмента dQ¯ осталась неизменной, то теплота процесса по изотерме, заменяющей верхнюю часть фрагмента произвольного цикла, окажется равной dQ. Далее, заменяя нижнюю часть фрагмента соответствующей изотермой с температурой Т2`, получим внутренний цикл Карно.
Термодинамический КПД цикла Карно, описанного вокруг произвольного цикла, обозначим he, а КПД цикла Карно, заменяющего фрагмент произвольного цикла, - hi.
Поскольку изотерма с температурой Т1 лежит выше изотермы с температурой Т1`, а изотерма с температурой Т2 находится ниже изотермы с температурой Т2`, то выполняются следующие неравенства:
T1>T1` , T2 <T2` ;
; 
; 
;
.
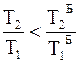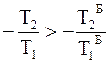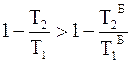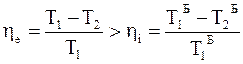Таким образом, термодинамический КПД любого фрагмента произвольного цикла всегда меньше КПД цикла Карно, проводимого при максимальной и минимальной температуре произвольного цикла. КПД всего произвольного цикла также должен быть меньше КПД цикла Карно, проводимого в том же температурном интервале.
Дата добавления: 2015-07-24; просмотров: 640;