Приведенные теплоты цикла Карно с идеальным газом. Температура как интегрирующий делитель в квазистатических процессах с идеальным газом

Приведенной теплотой называется отношение теплоты политропического процесса к температуре, при которой он проводится.

Строго этому определению удовлетворяет изотермический процесс. Однако если теплота других процессов является величиной очень малой, то можно рассматривать элементарную приведенную теплоту в виде dQ/T.

Как уже было показано, для квазистатического цикла Карно выполняется равенство

,

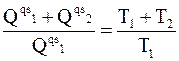в котором символ qs обозначает, что речь идет о теплоте квазистатического процесса.

Проведя несложные преобразования, получим

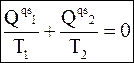. (3 - 20)

Равенство (3 - 20) означает, что

в проводимом квазистатическом цикле Карно сумма приведенных теплот всегда равна нулю.

Этот результат распространяется и на бесконечно малые циклы Карно, к которым относятся циклы с бесконечно малым расстоянием между изотермами (в этих циклах теплоты изотерм являются конечными величинами) или бесконечно малыми расстояниями между адиабатами (теплоты бесконечно малых изотерм также являются бесконечно малыми).

Для циклов Карно с бесконечно малым расстоянием между адиабатами выражение (3 - 20) можно записать в форме

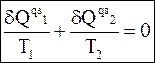(3 - 21)

Выше было показано, что совершаемый квазистатически произвольный цикл можно заменить бесконечно малыми изотермами, расположенными между соответствующими парами адиабат. Обход по всему произвольному циклу (по часовой стрелке) соответствует обходу справа налево по верхним изотермам (им соответствуют теплоты dQ^qs ₁ ) и слева направо по нижним изотермам (соответствуют теплоты dQ^qs ₂ ) . Поэтому, выбрав две точки 1 и 2 на контуре произвольного цикла (см. рис. 3- 3), можем записать

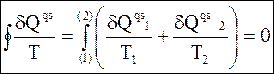(3 - 22)

Из равенства (3 - 22) следует, что величина dQ^qs /T представляет собой приращение некоторой функции, так как только в этом случае ее интеграл по замкнутому контуру равен нулю.

Получен замечательный результат:

в квазистатическом процессе с идеальным газом приведенная элементарная теплота совпадает с приращением некоторой функции.

Это означает, что по крайней мере для идеального газа изменение этой функции при переходе из одного и того же исходного состояния в одно и то же конечное состояние не зависит от процесса.

Существует также аналитический способ получения подобного результата для идеального газа.

Записав для идеального газа баланс энергии в форме

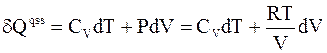
и разделив части равенства на Т, получим

.

Вследствие равенства частных производных

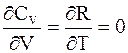
приведенная теплота является приращением функции состояния.

Таким образом, делением на температуру теплота, являющаяся характеристикой процесса, становится величиной, приращение которой от процесса не зависит. Температура приобретает свойство интегрирующего делителя для теплоты квазистатического процесса.

Свойство температуры как интегрирующего делителя нами установлено только для идеального газа. Возможность обобщения результата на любые системы выходит за пределы первого постулата термодинамики.