Политропические процессы с идеальным газом
В этой главе рассматриваются только квазистатические процессы в простых системах.
Политропическими процессами называются процессы, в ходе которых зависимость между параметрами имеет вид
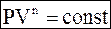. (3 - 8)
Уравнение (3 - 8) называется уравнением политропы, а показатель степени n - показателем политропы.
Другие формы уравнения политропы можно получить, если воспользоваться уравнением состояния идеального газа. Подставляя в уравнение (3 - 8) вместо давления RT/V, получим
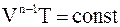, (3 - 9)
а подставляя V вместо RT/P, получим
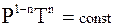. (3 - 10)
Для вывода уравнения политропы используем уравнение баланса энергии и свойства идеального газа:
dQ = dU + PdV;
dQ = CdT; dU = CvdT; dT = R-1(PdV + VdP); Cp - Cv = R.
Далее можно записать:
CdT = CvdT + PdV;
(C - Cv)dT = PdV;
(C - Cv)R-1(PdV + VdP) = PdV;
(C - Cv)( PdV + VdP) = RPdV = (Cp - Cv)PdV;
(C - Cv)VdP + (C - Cp)PdV = 0.
Разделив обе части последнего равенства на PV и на (C - Cp), получим:
.
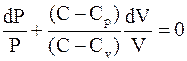Интегрирование приводит к следующему выражению:
.
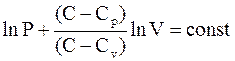Окончательная форма уравнения имеет следующий вид:
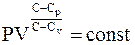. (3 - 11)
Сравнивая две формы записи уравнения политропы (3 - 8) и (3 - 11), находим, что показатель политропы определяется теплоемкостью процесса
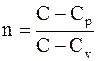. (3 - 12)
Рассмотрим, какие значения принимает показатель политропы для важнейших термодинамических процессов.
Изотермический процесс. Ранее было показано, что при приближении процесса к изотермическому его теплоемкость стремится к двум значениям: + ¥ или - ¥. Следовательно, показатель политропы стремится к 1.
Таким образом, уравнение изотермы
PV=const
является частным случаем политропы.
Изобарический процесс. Приближение процесса к изобарическому означает, что для его теплоемкости выполняется условие C ® Cp. Следовательно, n ® 0. В этом случае уравнение (3 - 9) примет вид
V-1T=const
или
,
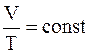что соответствует закону Гей-Люссака.
Изохорический процесс. Из условия C ® Cv следует, что n ® ¥ и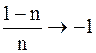 
. Переписав уравнение (3 - 10) в форме
,
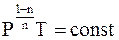получим
.
Последнее уравнение соответствует закону Шарля.
Адиабатический процесс. Для этого процесса выполняется условие C=0. Показатель степени становится равным
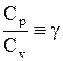. (3 - 13)
Вводимый равенством (3 - 13) показатель g называется показателем адиабаты.
Уравнение адиабаты, связывающее параметры идеального газа в адиабатическом процессе, имеет следующие формы:
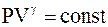, (3 - 14)
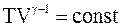, (3 - 15)
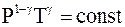. (3 - 16)
Уравнение адиабаты можно вывести, принимая, что теплота процесса dQ=CdT=0 и изменение внутренней энергии равно dU=CvdT. Исходное уравнение таково:
CvdT + PdV = 0.
Для его решения используются те же приемы, что и для вывода уравнения (3 - 11).
Дата добавления: 2015-07-24; просмотров: 1334;