Основные свойства идеального газа

Как уже указывалось, идеальный газ является воображаемой системой, которой приписываются определенные свойства. Прежде всего зависимость между параметрами идеального газа устанавливается уравнением состояния (напомним, что оно относится к 1 моль газа или смеси различных газов)

PV=RT (3 - 1)

Еще одно свойство газов при низких давлениях, т.е. приближающихся по свойствам к идеальному газу, было установлено Гей-Люссаком и подтверждено Джоулем и другими исследователями. Оно заключается в следующем.

Если газ быстро (без теплообмена) выпускать в пустоту, то его температура не изменится. При вытекании газа увеличивается его объем и падает давление. В то же время при истечении газа в пустоту он не испытывает сопротивления среды и, следовательно, не совершает работу. Отсутствие работы и теплообмена означает, что внутренняя энергия газа не изменяется.

Таким образом, не вызывающее изменения внутренней энергии истечение газа в пустоту влияет на объем и давление, но не влияет на температуру.

Внутренняя энергия идеального газа зависит только от темпера­туры.

Это утверждение, известное как закон Гей-Люссака - Джоуля, является вторым важнейшим свойством идеального газа.

Особенности идеального газа связаны также с его теплоемкостями.

Установлено, что теплоемкость газа при постоянном объеме C_v не зависит от температуры, но зависит от числа атомов, составляющих молекулу газа. В частности, для одноатомных молекул, к числу которых можно отнести атомы инертных газов, для теплоемкости С_v выполняется условие

, (3 - 2)

для двухатомных молекул -

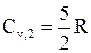, (3 - 3)

для молекул, состоящих из трех и более атомов -

. (3 - 4)

Используя уравнение состояния для идеального газа, его энтальпию можно выразить следующим образом:

H = U + RT. (3 - 5)

Изменение энтальпии можно записать так:

dH = dU + RdT. (3 - 6)

Из равенств (2 - 11) и (2 - 15) следует

C_pdT = C_vdT + RdT

или

C_p = C_v + R (3 - 7)

Равенство (3 - 7) известно под названием формулы Майера, выведшего ее в начале 40-х годов XIX в.