Параметры затухающих колебаний

1)Период затухающих колебаний:

Т = 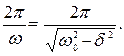(58)

При δ << ω_o колебания не отличаются от гармонческих: Т = 2π / ω_o.

2) Амплитуда затухающих колебанийвыражается формулой (119).

3) Декремент затухания, равный отношению двух последовательных амплитуд колебаний А(t) и А(t+Т), характеризует быстроту уменьшения амплитуды за период:

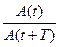= e^{d Т} (59)

4) Логарифмический декремент затухания - натуральныйлогарифм отношения амплитуд двух последовательных колебаний, соответст­вующих моментам времени, отличающимся на период

q = ln 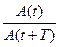= ln e^dТ =dT (60)

Логарифмический декремент затухания - по­стоянная для данной колебательной системы величина.

5) Временем релаксацииназывается промежуток времени (t) в течение которого амплитуда затухающих колебаний уменьшается в е раз:

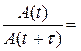e^{d τ} = е, δτ = 1,

t = 1/d, (61)

Из сравнения выражений (60) и (61) получим:

q = 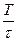= 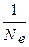, (62)

где N_e — число колебаний, совершаемых за время релаксации.

Если за время t система совершает Ν колебаний, то t = Ν^.Τ и уравнение затухающих колебаний можно представить в виде:

S = A₀ e^{-d N T} cos(w t+j )= A₀ e^{-q N} cos(w t+j ).

6)Добротностью колебательной системы (Q) называется величина, характеризующая потерю энергии в системе за период колебаний:

Q = 2p 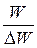, (63)

где W - полная энергия системы, ΔW - энергия, рассеянная за период. Чем меньше энергии рассеивается, тем больше добротность системы. Расчеты показывают, что

Q = 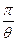= pN_e = 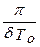= 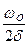. (64)

Таким образом, добротность обратно пропорциональна логарифмическому декременту затухания. Из формулы (64) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

7) Потенциальную энергию системы в момент t, можно выразить через потенциальную энергию W₀ при наибольшем отклонении:

W = 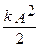= 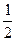kA_o² e^-2qN = W₀ e^-2qN. (65)

Обычно условно считают, что колебания практически прекратились, если их энергия уменьшилась в 100 раз ( амплитуда уменьшилась в 10 раз). Отсюда можно получить выражение для расчета числа колебаний, совершенных системой:

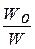= e^2qN = 100, ln100 = 2qN;

N = 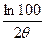= 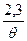. (66)