Сложение взаимно перпендикулярных колебаний

Рассмотрим результат сложения двух гармонических колебаний одинаковой час­тоты w, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

x =Acoswt

y =Bcos(wt+a) (45)

где a - разность фаз обоих колебаний, А и В — амплитуды складываемых колебаний. Для получения уравнения траектории результирующего колебания исключим из выражений (45) параметр t. Запишем складываемые колебания в виде

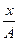= coswt; 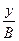= cos(wt+j) =coswt^.cosj - sinwt^.sinj;

т.к. coswt = 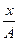, то sinwt ;

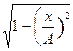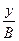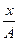= cosj - sinj ;

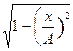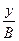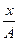- cosj = - sinj ;

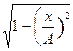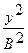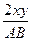- cosj + 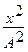cos²j = sin²j - 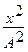sin²j;

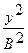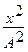+ ( cos²j + sin²j ) - 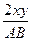cosj = sin²j;

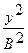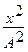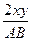+ - cosj = sin²j . (46)

это уравнение эллипса оси которого ориентированы относительно координатных осей произвольно. Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз φ. Рассмотрим некоторые частные случаи, представляющие физический интерес:

1) φ = mp ( m = 0, ±1, ± 2, …);

В данном случае эллипс вырождается в отрезок прямой

y = ± 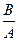x; (47)

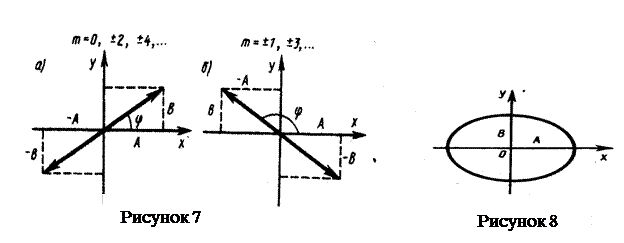
где знак плюс соответствует нулю и четным значениям т (рис.7а), а знак

минус — нечетным значениям т (рис. 7б). Результирующее колебание является гармоническим колебанием с

частотой w и амплитудой 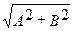, совершающимся вдоль прямой (47), составляющей с осью х угол

j = arctg ( 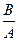cosmp).

Полученные колебания называются линейно поляризованными.

2) φ = (2m+1)p/2 ( m = 0, ±1, ± 2…)

В данном случае уравнение (45) примет вид:

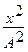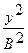+ = 1 (48)

Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рисунок 8). Кроме того, если А=В, то эллипс (48) вырождается в окружность. Такие колебания называютсяциркулярно поляризо­ванными колебаниями или колебаниями, поляризованными по кругу.

3) Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые тра­ектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называютсяфигурами Лиссажу.

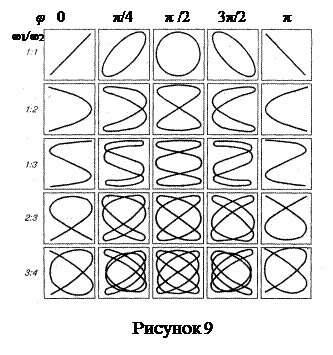
Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рисунке 9 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху).

Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной частоте или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу - широко используемый метод исследования соотношений частот и разности фаз.

ЛЕКЦИЯ 2