Гармонические колебания в колебательном контуре
Колебательный контур - цепь состоящая из включенных последовательно катушки 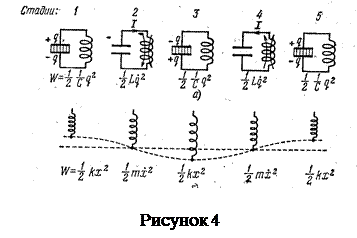 индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.
индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.
Для возбуждения в контуре колебаний конденсатор сначала заряжают, сообщая ему заряд ±q. Если R=0, то потерь энергии в контуре не будет, и колебания будут носить периодический незатухающий характер, т.е. заряд q
на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности, будут меняться по гармоническому закону. Электрические колебания в контуре сопровождаются. превращениями энергий электрического и магнитного полей. Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рисунок 28). Энергия электрического поля конденсатора q2/2С аналогична потенциальной энергии упругой деформации kx2/2, энергия магнитного поля катушки LI2/2 - кинетической энергии mV2/2, сила тока в контуре - скорости движения маятника. Индуктивность L играет роль массы m, а сопротивление контура - роль силы трения, действующей на маятник.
В соответствии со вторым законом Кирхгофа:
IR = Uc + εs, (29)
где IR -напряжение на резисторе. При R=0 IR = 0. 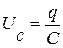 - напряжение на
- напряжение на
конденсаторе; 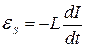 - э.д.с. самоиндукции, поэтому второй закон Кирхгофа примет вид:
- э.д.с. самоиндукции, поэтому второй закон Кирхгофа примет вид:
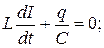
или:
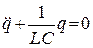 .
.
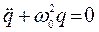 . (30)
. (30)
Из сравнения уравнений (30) и (8) следует, что при отсутствии сопротивления в колебательном контуре возникают гармонические колебания с частотой
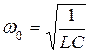 (31)
(31)
и периодом:
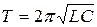 (32)
(32)
Формула (32) называется формулой Томсона.
Решение уравнения (30):
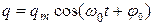
Сила тока в колебательном контуре
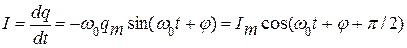 ,
,
где Im = w0 qm.. Колебания тока I опережают по фазе колебания заряда q на p/2.
Напряжение на конденсаторе:
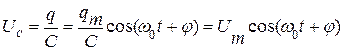 , где Um =
, где Um = 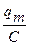 .
.
Дата добавления: 2015-07-18; просмотров: 2272;
