Дифференциальное уравнение гармонических колебаний

Согласно выражению (7) ускорение гармонических колебаний имеет вид:

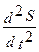= -Aw₀²cos(w₀t+j)

или: 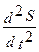= - w₀²Ѕ,

отсюда:

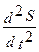+ w₀²S = 0. (8)

Однородное дифференциальное уравнение (8) является дифференциальным уравнением гармонических колебаний.Если какой-либо процесс описывается дифференциальным уравнением вида (70), он обязательно носит характер гармонических колебаний.

Решение уравнения (8) имеет вид:

S = A cos(w₀t+j)

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм (рис. 24). Вектор 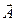откладывается из произвольной точки оси Х, под углом j₀, равным начальной фазе, и вращается с угловой скоростью w₀, при этом его проекция Ѕ совершает гармонические колебания . В момент времени t вектор А расположен по отношению к оси Х под углом φ=ω_οt+φ_ο.