Математический маятник. Математическим маятником называется тяжелая материальная точка, подвешенная на невесомой нерастяжимой нити
 Математическим маятником называется тяжелая материальная точка, подвешенная на невесомой нерастяжимой нити. Из определения
Математическим маятником называется тяжелая материальная точка, подвешенная на невесомой нерастяжимой нити. Из определения
следует, что математическим маятником может служить любое тело, размеры которого пренебрежимо малы по сравнению с длиной нити, на которой оно подвешено.
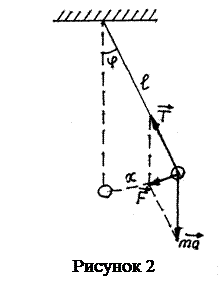
Пусть шарик массы m подвешен на невесомой нерастяжимой нити длиной 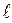 (рис.2). Если шарик вывести из положения равновесия, отклонив его на угол
(рис.2). Если шарик вывести из положения равновесия, отклонив его на угол 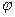 , то шарик будет совершать колебательное движение. Покажем, что при малых отклонениях колебания будут иметь гармонический характер.
, то шарик будет совершать колебательное движение. Покажем, что при малых отклонениях колебания будут иметь гармонический характер.
На шарик действуют сила тяжести 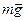 и сила натяжения нити
и сила натяжения нити 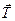 . Результирующая сила
. Результирующая сила 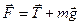 возвращает шарик к положению равновесия. По второму закону Ньютона
возвращает шарик к положению равновесия. По второму закону Ньютона
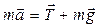 (15)
(15)
Из рисунка 2 следует:
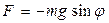 (16)
(16)
Знак (-) соответствует тому, что сила F направлена противоположено смещению шарика.
При малых углах 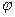
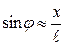 , где x – смещение от положения равновесия. Учитывая, что ускорение
, где x – смещение от положения равновесия. Учитывая, что ускорение  , из уравнений (15) и (16) получим:
, из уравнений (15) и (16) получим:
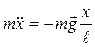 и
и 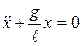 .
.
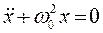 (17)
(17)
Уравнение (17) соответствует дифференциальному уравнению гармонических колебаний (8), следовательно, при малых отклонениях от положения равновесия математический маятник совершает гармонические колебания. Решение уравнения (17) имеет вид:
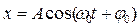 . (18)
. (18)
Из сравнения уравнений (17) и (8) следует:
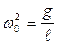 ,
, 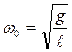 . (19)
. (19)
Выражение (19)– собственная частота колебаний математического маятника.
Период колебаний математического маятника
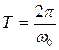 ,
, 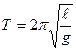 . (20)
. (20)
Таким образом, период колебаний математического маятника зависит от его длины 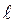 и не зависит ни от амплитуды колебаний, ни от массы маятника.
и не зависит ни от амплитуды колебаний, ни от массы маятника.
 4.1.5.3 Физический маятник
4.1.5.3 Физический маятник
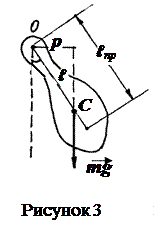
Физическим маятником называют твердое тело, совершающее колебания под действием силы тяжести относительно оси, не проходящей через центр тяжести тела (рисунок 3). При отклонении от положения равновесия на некоторый угол α, тело совершает колебательное движение с одной степенью свободы - α. На маятник действуют две силы: сила тяжести 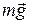 и сила реакции опоры в точке подвеса О. Относительно оси вращения, проходящей через точку О перпендикулярно плоскости чертежа, сила реакции не создает вращательного момента, а сила тяжести создает переменный момент, модуль которого равен:
и сила реакции опоры в точке подвеса О. Относительно оси вращения, проходящей через точку О перпендикулярно плоскости чертежа, сила реакции не создает вращательного момента, а сила тяжести создает переменный момент, модуль которого равен:
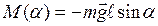 , (21)
, (21)
где ℓ - расстояние от точки подвеса О до центра тяжести тела С; р= ℓ sin α - плечо силы тяжести.Согласно основному закону динамики вращательного движения:
 , (22)
, (22)
где J - момент инерции тела относительно оси вращения, 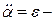 угловое ускорение тела.
угловое ускорение тела.
Из уравнений (21) и (22) следует:
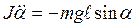 . (23)
. (23)
При малых отклонениях от положения равновесия sinα≈ α, поэтому:
 ,
,
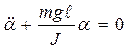 (24)
(24)
Из сравнения уравнений (24) и (8) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, дифференциальное уравнение которых
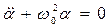 , (25)
, (25)
где 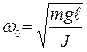 - циклическая частота колебаний физического маятника.
- циклическая частота колебаний физического маятника.
Период колебаний физического маятника
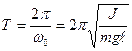 (26)
(26)
Величина 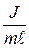 имеет размерность длины и называется приведенной длиной физического маятника ℓпр:
имеет размерность длины и называется приведенной длиной физического маятника ℓпр:
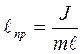 , (27)
, (27)
тогда
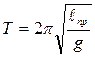 . (28)
. (28)
Из сравнения формулы (28) периода колебаний физического маятника с формулой периода колебаний математического маятника 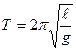 следует, что приведенной длиной физического маятника называют длину такого математического маятника, период которого равен периоду данного физического маятника.
следует, что приведенной длиной физического маятника называют длину такого математического маятника, период которого равен периоду данного физического маятника.
Дата добавления: 2015-07-18; просмотров: 3061;
