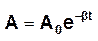Крутильний маятник
Крутильний маятник – це тверде тіло, закріплене на жорсткій підвісці, яке може здійснювати крутильні коливання під дією сил пружності деформації кручення підвіски .
При закручуванні маятника на кут 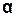 виникає момент пружної сили, який намагається повернути маятник у положення рівноваги
виникає момент пружної сили, який намагається повернути маятник у положення рівноваги
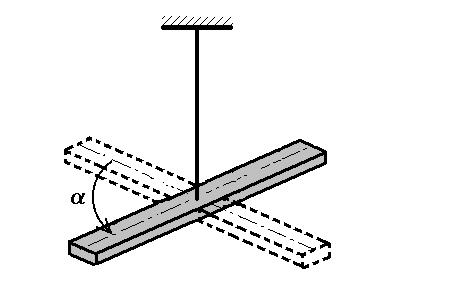
M = - f 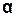 , (3.24)
, (3.24)
 |
де f - модуль кручення дротини, який залежить від розмірів
і пружних властивостей матеріалу дротини.
|
Оскільки після закручування маятник буде здійснювати обертальний рух навколо своєї вертикальної осі, яка проходить через точку підвісу вздовж дротини, то:
 M= J
M= J 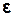 ,(3.25)
,(3.25)
де J– момент інерції маятника відносно осі закручування.
Врахувавши (3.13), (3.24), рівняння (3.25) запишемо у вигляді:
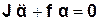 , (3.26)
, (3.26)
або:
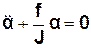 . (3.27)
. (3.27)
Ввівши позначення :
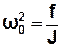 , (3.28)
, (3.28)
отримаємо диференціальне рівняння гармонічних коливань крутильного маятника:
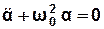 . (3.29)
. (3.29)
Розв’язком (3.28) є рівняння гармонічних коливань:
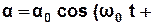 φ0). (3.30)
φ0). (3.30)
Період коливань крутильного маятника:
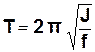 . (3.31)
. (3.31)
3.6. Згасаючі коливання
Реальні механічні коливання здійснюються при наявності сил опору середовища. Тому механічна енерґія коливної системи з часом зменшується, а самі коливання загасають. Сила опору середовища переважно пропорційна швидкості руху тіла, що здійснює коливання:
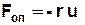 , (3.32)
, (3.32)
де r – коефіцієнт опору середовища,
знак ( - ) вказує на протилежний напрям сили опору
і швидкості руху.
Нехай тіло масою m під дією пружної сили -kxі сили опору 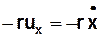 здійснює коливання вздовж осі OX. Рівняння руху такого тіла:
здійснює коливання вздовж осі OX. Рівняння руху такого тіла:
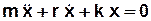 , (3.33)
, (3.33)
або: 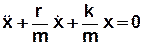 . (3.34)
. (3.34)
Позначивши:
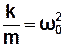 ;
; 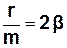 ,
,
де 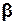 - коефіцієнт згасання,
- коефіцієнт згасання,
запишемо диференціальне рівняння згасаючих коливань:
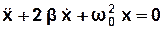 . (3.35)
. (3.35)
Якщо 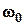 >
> 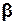 ,розв’язком (3.35) є рівняння:
,розв’язком (3.35) є рівняння:
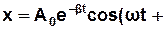 φ0), (3.36)
φ0), (3.36)
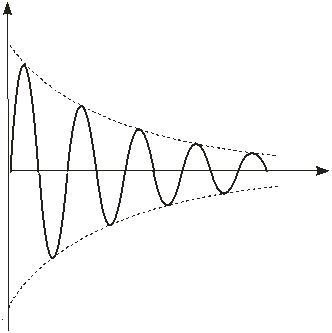
яке описує гармонічні коливання з циклічною частотою 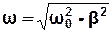 і змінною у часі амплітудою
і змінною у часі амплітудою 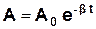 при початко-
при початко-
вій амплітуді А0 (рис.3.4)
|



|

|
|
|
|
|
|
|
Період згасаючих коливань: 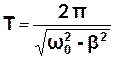 . (3.37)
. (3.37)
· Декрементом згасання D називається відношення амплітуд двох послідовних коливань:
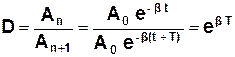 . (3.38)
. (3.38)
· Лоґарифмічним декрементом згасання називається фізична величина:
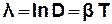 . (3.39)
. (3.39)
· Часом релаксації коливальної системи 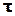 називається проміжок часу протягом якого амплітуда коливань зменшується в е разів (е– основа натурального лоґарифму)
називається проміжок часу протягом якого амплітуда коливань зменшується в е разів (е– основа натурального лоґарифму)
· Коефіцієнтом згасання називається фізична величина, обернена до часу релаксації:
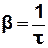 . (3.40)
. (3.40)
· Nе – число коливань, після здійснення яких амплітуда зменшується в е разів, так що 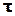 =NеT.
=NеT.
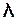 =
=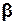 Т=
Т= 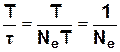 .(3.41)
.(3.41)
Отже лоґарифмічний декремент згасання - це фізична величина, обернена до числа коливань Ne, після здійснення яких амплітуда зменшується в е разів.
· Добротністю системи називається фізична величина:
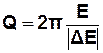 ,(3.42)
,(3.42)
де Е – енерґія системи у даний момент часу;
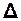 E – енерґія, втрачена протягом одного періоду.
E – енерґія, втрачена протягом одного періоду.
Отже добротність системи тим більша, чим менші втрати
енерґії системи 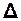 E.Можна показати, що:
E.Можна показати, що:
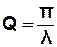 =
= 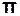 Ne . (3.43)
Ne . (3.43)
3.7. Механічні хвилі
Хвиля – це процес поширення коливань у просторі. При поширенні хвилі частинки середовища не втягуються у поступальний рух, а лише коливаються навколо положень рівноваги. При цьому частинки обмінюються енерґією. Тому хвилі переносять енерґію без перенесення речовини.
Механічні (пружні) хвилі - це процес поширення коливань у пружному середовищі. Хвилі бувають поздовжніми і поперечними.
У випадку поперечної хвилі частинки середовища коливаються в напрямі, перпендикулярному до напряму поширення хвилі. Поперечні хвилі поширюються у середовищах, в яких виникають пружні сили при деформації зсуву, тобто в твердих тілах. Поперечна хвиля може поширюватися також на поверхні рідини.
Швидкість поширення поперечної хвилі:
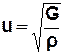 , (3.44)
, (3.44)
де G – модуль зсуву,
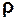 - густина середовища.
- густина середовища.
У випадку поздовжньої хвилі частинки середовища коливаються у напрямі поширення хвилі. Поздовжні хвилі поширюються у середовищах, де виникають пружні сили при
деформаціях стиску (розтягу), тобто у твердих тілах, рідинах і газах. Швидкість поширення поздовжньої хвилі:
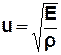 , (3.45)
, (3.45)
де Е – модуль Юнґа,
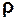 - густина середовища.
- густина середовища.
Для опису хвиль поряд з такими характеристиками, як амплітуда, період, частота, фаза використовують поняття:
· хвильовий фронт – ґеометричне місце точок середовища, до яких доходять коливання в даний момент часу;
· хвильова поверхня – ґеометричне місце точок, які коливаються в однаковій фазі. За формою хвильової поверхні розрізняють плоскі, сферичні і інші хвилі;
· промінь –лінія, перпендикулярна до хвильової поверхні;
· довжина хвилі (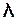 ) – найменша відстань між двома точками середовища у напрямі, перпендикулярному до напряму поширення, які коливаються в однаковій фазі;
) – найменша відстань між двома точками середовища у напрямі, перпендикулярному до напряму поширення, які коливаються в однаковій фазі;
· швидкість хвилі (u) – швидкість поширення постійної фази хвилі;
· хвильове число - 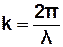 .
.
Довжина хвилі, швидкість, період і частота n зв’язані співвідношеннями:
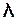 =uT;
=uT;
u= 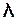 ν.
ν.
Плоска біжуча хвиля
Хвилі, які переносять у просторі енерґію, називаються біжучими. Якщо плоска хвиля поширюється вздовж осі OX, то 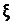 -зміщення з положення рівноваги частинок, що коливаються, залежить від їхніх координат x та часу t, тобто
-зміщення з положення рівноваги частинок, що коливаються, залежить від їхніх координат x та часу t, тобто 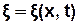 .
.
|
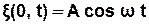 , то частинка В коливатиметься за таким же законом, але її коливання будуть запізнюватися у часі порівняно з коливаннями джерела на
, то частинка В коливатиметься за таким же законом, але її коливання будуть запізнюватися у часі порівняно з коливаннями джерела на 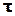
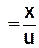
|
|


| |
|
|
|
|


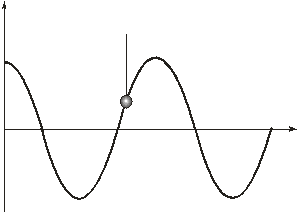

Тому рівняння біжучої хвилі має вигляд:
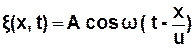 . (3.46)
. (3.46)
Якщо плоска хвиля поширюється у протилежному напрямі, то:
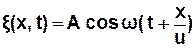 . (3.47)
. (3.47)
У загальному випадку:
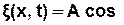 [
[ 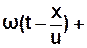 φ0] . (3.48)
φ0] . (3.48)
Враховуючи :
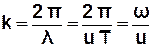 ,
,
надамо рівнянню плоскої хвилі вигляду:
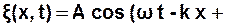 φ0). (3.49)
φ0). (3.49)
Інтерференція хвиль. Стоячі хвилі.
Хвилі називаються когерентними, якщо вони мають однакову частоту і різниця їх фаз залишається постійною в часі:
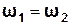
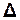 φ = (φ1 – φ2)
φ = (φ1 – φ2)
Інтерференція – це явище перерозподілу енергії хвиль в просторі з утворенням стійких в часі областей максимуму і мінімуму енерґії, яке відбувається в результаті накладання когерентних хвиль.
Особливим випадком інтерференції є утворення стоячих хвиль.
Стоячі хвилі – це результат накладання двох біжучих когерентних хвиль з однаковими амплітудами, які поширюються назустріч одна одній:
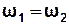 ;
; 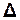 φ
φ 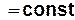 ;
; 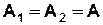 .
.
Рівняння вказаних хвиль відповідно мають вигляд:
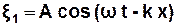 ; (3.50)
; (3.50)
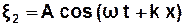 . (3.51)
. (3.51)
При додаванні цих рівнянь отримаємо рівняння стоячої хвилі:

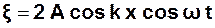 (3.52)
(3.52)
Амплітуда стоячої хвилі залежить від координати x:
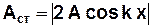 . (3.53)
. (3.53)
В точках середовища, де
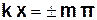 (m = 0, 1, 2, …),(3.54)
(m = 0, 1, 2, …),(3.54)
амплітуда Аст досягає максимального значення, яке дорівнює 2А.
Ці точки називаються пучностями стоячої хвилі.
В точках середовища, де
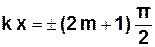 (m = 0, 1, 2, …),(3.55)
(m = 0, 1, 2, …),(3.55)
амплітуда Аст=0.
Ці точки називаються вузлами стоячої хвилі.
З рівнянь (3.54) і (3.55) отримаємо координати пучностей та вузлів:
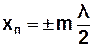 ; (3.56)
; (3.56)
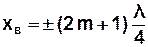 . (3.57)
. (3.57)
Відстань між двома сусідніми вузлами (або пучностями) стоячої хвилі називають довжиною стоячої хвилі 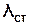 :
:
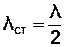 . (3.58)
. (3.58)
Всі точки стоячої хвилі між двома вузлами коливаються з різними амплітудами, але з однаковими фазами.
Стояча хвиля не переносить енерґію, тому що падаюча і відбита хвилі однакової амплітуди несуть однакову енерґію в протилежних напрямках.
Якщо середовище, від якого відбувається відбивання, менш густе, то в місці відбивання отримується пучність, якщо більш густе – вузол.
Дата добавления: 2015-07-24; просмотров: 1702;