Гармонічний осцилятор. Пружинний, фізичний і математич-ний маятники
Гармонічним осцилятором називається система, яка описується диференціальним рівнянням вигляду (6):
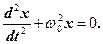 (16)
(16)
Коливання гармонічного осцилятора є важливим прикладом періодичного руху і служать точною або наближеною моделлю в багатьох задачах класичної і квантової фізики. Прикладами гармонічного осцилятора є пружинний, фізичний і математичний маятники, коливальний контур (для струмів і напруг настільки малих, щоб елементи контуру можна було вважати лінійними).
Пружинний маятник. Пружинний маятник – невеличке тіло масою т, яке підвішене до абсолютно пружної пружині і здійснює гармонічні коливання під дією пружної сили F = - kx, де k - коефіцієнт пружності, у випадку пружини, названий жорсткістю (рис. 4).

Рис.4
Диференціальне рівняння коливання маятника буде мати вигляд
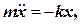
або
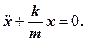 (17)
(17)
З виразів (16) і (1) випливає, що пружинний маятник виконує гармонічні коливання за законом  з циклічною частотою
з циклічною частотою 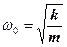 і періодом
і періодом 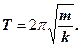
Формула (17) справедлива для пружних коливань у межах, для яких виконується закон Гука, тобто коли маса пружини мала в порівнянні з масою тіла.
В цьому випадку потенціальна енергія пружинного маятника, згідно з (13) дорівнює
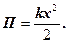 (18)
(18)
Фізичний маятник. Фізичний маятник – тверде тіло, яке під дією сили тяжіння виконує гармонічні коливання відносно нерухомої горизонтальної осі, що проходить через точку підвішування і яка не збігається з центром мас С тіла (рис. 5).
Якщо маятник відхилений від положення рівноваги на деякий кут  , то відповідно до основного рівняння динаміки обертального руху твердого тіла момент Μ сили Fτ, яка повертає маятник до положення рівноваги буде дорівнювати
, то відповідно до основного рівняння динаміки обертального руху твердого тіла момент Μ сили Fτ, яка повертає маятник до положення рівноваги буде дорівнювати
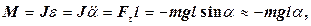 (19)
(19)
де J – момент інерції маятника відносно осі, яка проходить через точку О;
l – відстань між точкою підвішування і центром мас маятника;
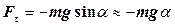 – сила, яка повертає маятник у попереднє положення, (знак мінус обумовлений тим, що зростання
– сила, яка повертає маятник у попереднє положення, (знак мінус обумовлений тим, що зростання 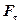 і швидкості
і швидкості 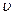 завжди протилежні;
завжди протилежні;
sinα 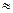 α – відповідає малим коливанням маятника, тобто малим відхиленням маятника від положення рівноваги.
α – відповідає малим коливанням маятника, тобто малим відхиленням маятника від положення рівноваги.

Рис. 5
Рівняння (19) можна записати у вигляді
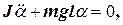
або
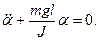
Приймаючи, що 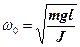 одержимо рівняння
одержимо рівняння 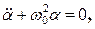 ідентичне з (16), розв’язком якого є функція:
ідентичне з (16), розв’язком якого є функція:
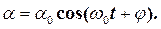 (20)
(20)
З виразу (20) випливає, що при малих коливаннях фізичний маятник виконує гармонічні коливання з циклічною частотою 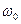 і періодом
і періодом
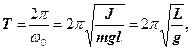 (21)
(21)
де 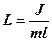 – зведена довжина фізичного маятника.
– зведена довжина фізичного маятника.
Точка 0' на продовженні прямої 0С, якавідстоїть від осі підвішування на відстані зведеної довжини L, називається центром коливань фізичного маятника (рис. 5). Застосовуючи теорему Штейнера, можна показати, що 00' завжди більше 0С = l. Точка підвішування 0 і центр коливань 0' мають властивість взаємозамінності, якщо вісь підвішування перенести в центр коливань, то точка 0, в якійрозміщувалась раніше вісь підвішування стане новим центром коливань і період коливань фізичного маятника не зміниться.
Математичний маятник.Математичний маятник – ідеалізована система, яка складається з матеріальної точки масою т, підвішеної на нерозтяжній невагомій нитці, і коливається під дією сили тяжіння (рис.6).
Гарним наближенням математичного маятника є невелика важка кулька, підвішена на тонкій довгій нитці. Момент інерції математичного маятника дорівнює
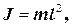 (22)
(22)
де l - довжина маятника.

Рис. 6
Оскільки математичний маятник можна подати як окремий випадок фізичного маятника, припустивши, що вся маса фізичного маятника зосереджена в одній точці – центрі мас, то, підставивши вираз (22) у формулу (21), одержимо знайомий вираз для малих коливань математичного маятника:
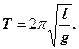 (23)
(23)
Порівнюючи формули (23) і (21), бачимо, що якщо зведена довжина L фізичного маятника дорівнює довжині l математичного маятника, то їх періоди коливань збігаються. Отже, зведена довжина фізичного маятника – це довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника.
Дата добавления: 2015-08-26; просмотров: 1669;
