Додавання взаємно перпендикулярних коливань. Фігури Ліссажу

Нехай матеріальна точка С одночасно бере участь у двох гармонічних коливаннях з однаковою циклічною частотою у взаємо перпендикулярних напрямках (рис. 4).

Рис.4

При збудженні коливань матеріальна точка С буде рухатись по деякій криволінійній траєкторії, форма якої залежить від різниці фаз обох коливань.

Рівняння коливань точки в напрямках осі x і осі y матимуть вигляд

(23)

де 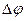– спільна різниця фаз цих коливань.

Щоб отримати рівняння траєкторії у звичайному вигляді, треба виключити з цих рівнянь час t.

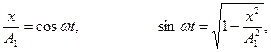
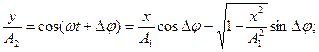
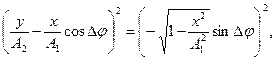
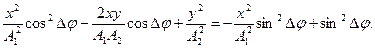
В результаті отримаємо

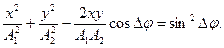(24)

Рівняння (24) є рівнянням траєкторії результуючого коливання точки С. Це рівняння є еліпсом, осі якого повернуті відносно осей x і y. Орієнтація еліпса і величина його півосей залежить від амплітуд 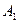і 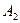і різниці фаз .

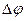Розглянемо окремі випадки.

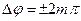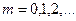1. Нехай , де Тоді

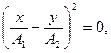
звідки

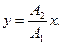(25)

Результуюче коливання є гармонічним коливанням вздовж прямої з частотою ω і амплітудою 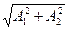(рис.5).

Рис.5

Пряма утворює з віссю x кут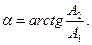

2. Нехай 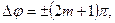де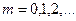

У цьому випадку

звідки

(26)

Результуючий рух – це гармонічне коливання вздовж прямої 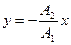(рис.6).

3. Нехай 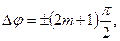де 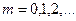В результаті одержуємо рівняння

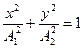(27)

Це рівняння еліпса, осі якого збігаються з осями координат, а його півосі дорівнюють відповідним амплітудам (рис. 7). Якщо 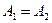, то еліпс перетворюється в коло.

Рис.6

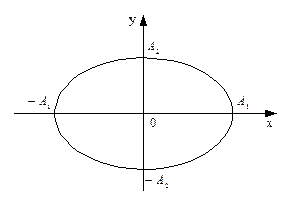
Рис.7

Два окремі випадки 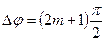і 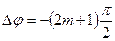відрізняються напрямком коливання по еліпсу або по колу. У випадку, коли циклічні частоти взаємно перпендикулярних коливань, що додаються, різні, то замкнута траєкторія результуючого коливання досить складна.

Замкнуті траєкторії, які рисуються одночасно коливальною точкою у взаємно перпендикулярних напрямках, називаються фігурами Ліссажу. Форма цих кривих залежить від співвідношення амплітуд, частот і різниці фаз коливань, які додаються.

На рис. 8 показана одна із найпростіших траєкторій, одержаних при додаванні взаємно перпендикулярних коливань з відношенням циклічних частот 1:2 і різниці фаз 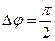. Рівняння коливань мають вигляд:

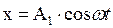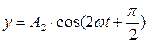, . (28)

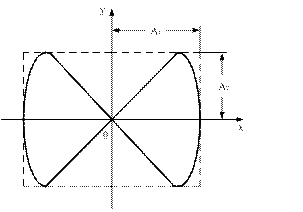
Рис. 8

Якщо відношення частот 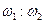дорівнює 1:2, а різниця фаз 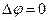, то траєкторія коливань точки вироджується в незамкнуту криву (рис. 9), вздовж якої рухається точка то в одну то в протилежну сторони.

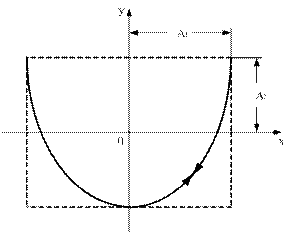
Рис. 9

Чим ближче до одиниці буде відношення частот 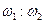, тим складнішою буде фігура Ліссажу. Для прикладу на рис. 10 наведена крива фігури Ліссажу з відношенням частот 3:4 і різницею фаз .

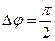Рис. 10