Вільні гармонічні коливання у коливальному контурі
Серед різних електричних явищ особливе місце займають електромагнітні коливання, при яких фізичні величини (заряди, струми, електричні і магнітні поля) періодично змінюються. Для виникнення і підтримування електромагнітних коливань необхідні певні системи, найпростішою з який є коливальний контур – ланцюг, який складається з увімкнених послідовно котушки індуктивністю L, конденсатора ємністю С і резистора опором R.
Розглянемо послідовні стадії коливального процесу в ідеалізованому контурі, опір якого безмежно малий 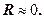 Для виникнення в контурі коливань конденсатор попередньо заряджають, надаючи його обкладкам заряди
Для виникнення в контурі коливань конденсатор попередньо заряджають, надаючи його обкладкам заряди 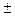 Q. Тоді в початковий момент часу
Q. Тоді в початковий момент часу 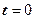 (рис. 5, а) між обкладками конденсатора виникне електричне поле, енергія якого
(рис. 5, а) між обкладками конденсатора виникне електричне поле, енергія якого
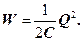
Замкнувши конденсатор на котушку індуктивності, він почне розряджатися й у контурі потече зростаючий з часом струм I. У результаті енергія електричного поля буде зменшуватися, а енергія магнітного поля котушки – зростати.
Оскільки 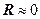 , то, відповідно до закону збереження енергії, повна енергія контуру буде дорівнювати
, то, відповідно до закону збереження енергії, повна енергія контуру буде дорівнювати
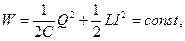
тому що енергія на нагрівання провідників у такому коливальному контурі не витрачається. У момент часу 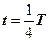 , коли конденсатор повністю розрядиться, енергія електричного поля зменшується до нуля, а енергія магнітного поля, а отже і струм досягають найбільшого значення (рис. 5,б). Починаючи з цього моменту часу струм у контурі буде зменшуватися; отже, почне слабшати магнітне поле котушки й індукований у ній струм, який тече (відповідно до правила Ленца) у тому ж напрямку, що й струм розрядки конденсатора. Конденсатор почне перезаряджатися, при цьому виникне електричне поле, яке намагатиметься послабити струм, який зрештою зменшується до нуля, а заряд на обкладках конденсатора досягне максимуму (рис. 5, в). Далі ті ж процеси почнуть протікати в зворотному напрямку (рис. 5, г) і система до моменту часу t = Τ прийде в початковий стан (рис. 5, а). Після цього почнеться повторення розглянутого циклу розрядки і зарядки конденсатора.
, коли конденсатор повністю розрядиться, енергія електричного поля зменшується до нуля, а енергія магнітного поля, а отже і струм досягають найбільшого значення (рис. 5,б). Починаючи з цього моменту часу струм у контурі буде зменшуватися; отже, почне слабшати магнітне поле котушки й індукований у ній струм, який тече (відповідно до правила Ленца) у тому ж напрямку, що й струм розрядки конденсатора. Конденсатор почне перезаряджатися, при цьому виникне електричне поле, яке намагатиметься послабити струм, який зрештою зменшується до нуля, а заряд на обкладках конденсатора досягне максимуму (рис. 5, в). Далі ті ж процеси почнуть протікати в зворотному напрямку (рис. 5, г) і система до моменту часу t = Τ прийде в початковий стан (рис. 5, а). Після цього почнеться повторення розглянутого циклу розрядки і зарядки конденсатора.
Якби втрат енергії не було, то в контурі відбувалися б періодичні незагасаючі коливання, тобто періодично змінювалися (коливалися) б заряд Q на обкладках конденсатора, напруга U на конденсаторі і сила струму I, яка тече через котушку індуктивності.
Отже, у контурі виникають електричні коливання з періодом Т, причому протягом першої половини періоду струм тече в одному напрямку, протягом другої половини – у зворотному. Коливання супроводжуються перетвореннями енергій електричних і магнітних полів.
Електричні коливання у коливальному контурі можна зіставити з механічними коливаннями маятника (рис. 7), які супроводжуються взаємними перетвореннями потенціальної і кінетичної енергій маятника.
У даному випадку потенціальна енергія маятника 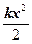 аналогічна енергії електричного поля конденсатора
аналогічна енергії електричного поля конденсатора 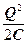 , кінетична енергія маятника
, кінетична енергія маятника 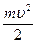 – енергії магнітного поля котушки
– енергії магнітного поля котушки 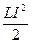 , а швидкість руху маятника – силі струму в контурі.
, а швидкість руху маятника – силі струму в контурі.
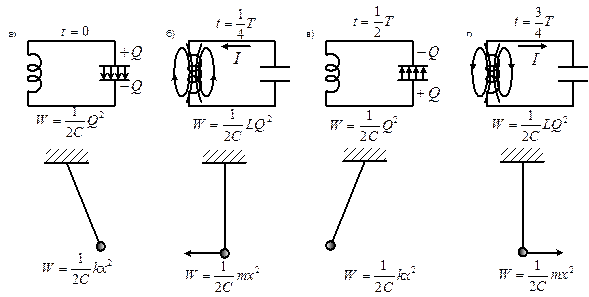
Рис.7
Роль інерції маятника буде зводитися до самоіндукції котушки, а роль сили тертя, яке діє на маятник – до опору контуру.
Відповідно до другого правила Кірхгофа, для контуру, який містить котушку індуктивністю L, конденсатор ємністю С і резистор опором R маємо
 ,
,
де IR – спад напруги на резисторі;
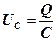 – напруга на конденсаторі;
– напруга на конденсаторі;
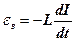 – е.р.с. самоіндукції, яка виникає в котушці при протіканні в ній змінного струму (
– е.р.с. самоіндукції, яка виникає в котушці при протіканні в ній змінного струму ( 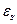 - єдина е.р.с. у контурі).
- єдина е.р.с. у контурі).
Отже,
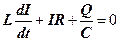 . (24)
. (24)
Розділивши (24) на L і підставивши 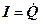 і
і 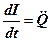 , одержимо диференціальне рівняння коливань заряду Q у контурі:
, одержимо диференціальне рівняння коливань заряду Q у контурі:
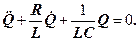 (25)
(25)
У даному коливальному контурі зовнішні е. р. с. відсутні, тому розглянуті коливання є вільнимиколиваннями. Якщо опір R = 0, то вільні електромагнітні коливання у контурі є гармонічними. Тоді з (25) одержимо диференціальне рівняння вільних гармонічних коливань заряду Q в контурі:
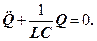 (26)
(26)
З виразу (26) випливає, що заряд Q в коливальномуконтурі виконує гармонічні коливання за законом
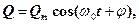 (27)
(27)
де Qm – амплітуда коливань заряду конденсатора з циклічною частотою ω0, яка називається власною частотою контуру:
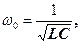 (28)
(28)
і періодом
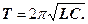 (29)
(29)
Формула (29) вперше була отримана Томсоном і називається формулою Томсона.
Сила струму в коливальному контурі буде дорівнювати
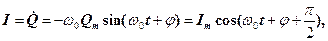 (30)
(30)
де 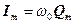 – амплітуда сили струму.
– амплітуда сили струму.
Напруга на конденсаторі
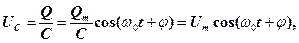 (31)
(31)
де 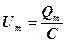 — амплітуда напруги.
— амплітуда напруги.
З виразів (30) і (31) випливає, що коливання струму I випереджають за фазою коливання заряду Q на π/2, тобто коли струм досягає максимального значення, заряд (також і напруга) зменшуються до нуля і навпаки.
Цей взаємозв'язок був установлений при розгляді послідовних стадій коливального процесу в контурі і на підставі енергетичних міркувань. Вільні електромагнітні коливання в контурі є незгасаючими.
Дата добавления: 2015-08-26; просмотров: 1789;
