Механічні гармонічні коливання
Нехай матеріальна точка виконує прямолінійні гармонічні коливання уздовж осі координат x біля положення рівноваги, прийнятого за початок координат. Тоді залежність координати x від часу t задається рівнянням (1),
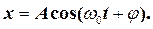 (9)
(9)
Відповідно до виразів (4) і (5) швидкість 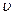 і прискорення а коливної точки будуть дорівнювати:
і прискорення а коливної точки будуть дорівнювати:

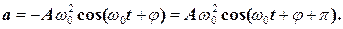 (10)
(10)
Сила F = ma, що діє на коливну матеріальну точку масою т, у відповідності з рівнянням (1) дорівнює
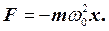
Отже, сила, яка діє на матеріальну точку при гармонічних коливаннях, пропорційна зміщенню матеріальної точки від положення рівноваги і спрямована в протилежну сторону.
Кінетична енергія матеріальної точки, яка здійснює прямолінійні гармонічні коливання, дорівнює
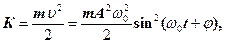 (11)
(11)
або
К = 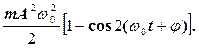 (12)
(12)
Потенціальна енергія матеріальної точки, яка здійснює гармонічні коливання під дією пружної сили F, дорівнює
П = -  (13)
(13)
або
П =  (14)
(14)

Рис. 3
Додавши (13) і (14), одержимо формулу для повної енергії гармонічного коливання:
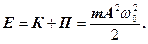 (15)
(15)
З формул (12) і (14) видно, що К і Π змінюються в часі з частотою, яка у два рази перевищує частоту гармонічного коливання. На рис. 3 показані графіки залежності х, К і Π від часу.
Оскільки середні значення 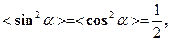 то з формул (11), (13) і (15) випливає, що
то з формул (11), (13) і (15) випливає, що
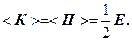
Дата добавления: 2015-08-26; просмотров: 1433;
