Фізичний зміст найбільш поширених параметрів чотириполюсників та їх еквівалентні схеми.
Розглянемо систему Z-параметрів.
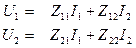 . (4.1)
. (4.1)
Очевидно , що 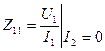 ,
, 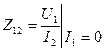 ,
, 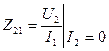 ,
, 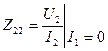 .
.
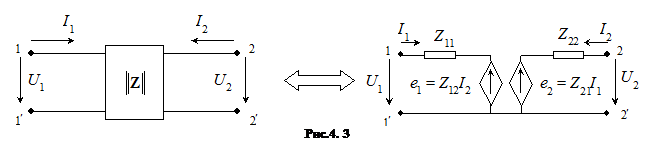
Оскільки Z- параметри визначаються при відсутності струму то їх часто називають параметрами холостого ходу. Задача синтезу на основі системи рівнянь (4.1) дозволяє побудувати еквівалентну схему чотириполюсника (рис.4.3)
Фізичну інтерпретацію 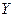 - параметрів отримаємо із відповідної системи рівнянь, а саме
- параметрів отримаємо із відповідної системи рівнянь, а саме
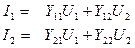 . (4.2)
. (4.2)
Звідки - 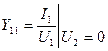 ,
, 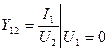 ,
, 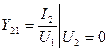 ,
, 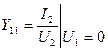 .
.
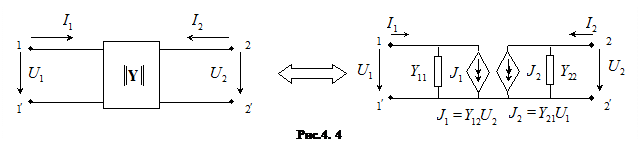 |
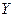 - параметри також називаються параметрами короткого замикання, оскільки вони визначаються в режимах короткого замикання на вході чи на виході.. Еквівалентна схема чотириполюсника з відомими
- параметри також називаються параметрами короткого замикання, оскільки вони визначаються в режимах короткого замикання на вході чи на виході.. Еквівалентна схема чотириполюсника з відомими 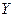 - параметрами має вигляд (див.рис.4.4):
- параметрами має вигляд (див.рис.4.4):
При аналізі схем з електронними лампами та напівпровідниковими транзисторами особливо корисна математична модель чотириполюсника, що описується 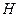 - параметрами
- параметрами
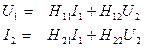 . (4.3)
. (4.3)
Звідки - 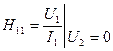 ,
, 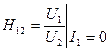 ,
, 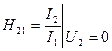 ,
, 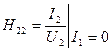 .
.
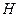 - параметри, це гібридні параметри, оскільки два із них визначаються в режимі холостого ходу, а інші два - в режимі короткого замикання. Еквівалентна схема чотириполюсника, який характеризується
- параметри, це гібридні параметри, оскільки два із них визначаються в режимі холостого ходу, а інші два - в режимі короткого замикання. Еквівалентна схема чотириполюсника, який характеризується 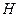 - параметрами має вигляд (див.рис.4.5)
- параметрами має вигляд (див.рис.4.5)

Параметри з індексами 11 називаються вхідними опорами або провідностями, а з індексами 22 - вихідними. Визначаються вони у режимах холостого ходу і короткого замикання на протилежній стороні чотириполюсника. Так, 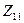 - вхідний опір при холостому ході на виході,
- вхідний опір при холостому ході на виході, 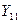 - вхідна провідність при короткому замиканні на виході,
- вхідна провідність при короткому замиканні на виході, 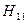 - вхідний опір при короткому замиканні на виході. Очевидно, що
- вхідний опір при короткому замиканні на виході. Очевидно, що 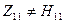 .
.
Параметри з індексами 21 називаються передаточними від входу до виходу, і вказують на характер перетворення вхідного сигналу у відповідний вихідний. Наприклад, параметр 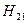 - підсилення струму при короткому замиканні на виході. Параметри з індексами 12 називаються передаточними із виходу на вхід і характеризують вплив виходу на вхідні сигнали. Якщо параметри з індексами12 дорівнюють нулеві то вплив відсутній.
- підсилення струму при короткому замиканні на виході. Параметри з індексами 12 називаються передаточними із виходу на вхід і характеризують вплив виходу на вхідні сигнали. Якщо параметри з індексами12 дорівнюють нулеві то вплив відсутній.
Оскільки різними параметрами можна характеризувати один і той чотириполюсник то між ними повинен бути зв’язок, іншими словами - одні параметри можна виразити через інші. Особливо легко установити такий зв’язок використовуючи матричні методи. Насправді, нехай чотириполюсник описується 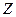 -параметрами. Тоді в матричному вигляді маємо
-параметрами. Тоді в матричному вигляді маємо 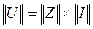 . Помножимо зліва ліву та праву частину даного виразу на матрицю
. Помножимо зліва ліву та праву частину даного виразу на матрицю 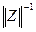 обернену матриці
обернену матриці 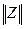 :
: 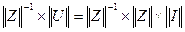 . Оскільки добуток
. Оскільки добуток 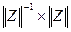 є одиничною матрицею, то отримаємо -
є одиничною матрицею, то отримаємо -  . Останнє матричне рівняння співпадає за формою з матричним рівнянням для системи
. Останнє матричне рівняння співпадає за формою з матричним рівнянням для системи 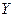 - параметрів:
- параметрів: 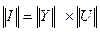 . Звідси -
. Звідси -  .Щоб побудувати елементи оберненої матриці необхідно:
.Щоб побудувати елементи оберненої матриці необхідно:
1. Побудувати додаткову матрицю елементами якої є алгебраїчні доповнення (мінори із знаком).
2. Транспонувати додаткову матрицю (стовпчики замінити на строчки).
3. Елементи отриманої матриці поділити на детермінант основної.
Здійснивши вказані операції отримаємо:
 ,
, 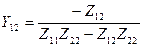 ,
, 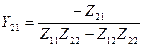 ,
, 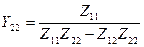 .
.
Дата добавления: 2015-08-14; просмотров: 1086;
