Частотні характеристики навантаженого чотириполюсника.

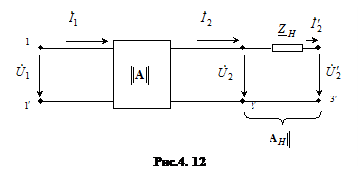
Доповнимо чотириполюсник його оточенням: генератором та навантаження. В цьому випадку лінійна модель пристрою показана на рис.4.11 Знайдемо вхідний опір. Скористаємося матричним методом. За означенням . Подамо чотириполюсник з під’єднаним до нього навантаженням у вигляді двох каска дно сполучених чотириполюсників (рис.4.12). Очевидно, що якщо за коротити затискачі , то вказане сполучення чотириполюсників відповідатиме ситуації показаній на рис.4.11. Матриця А-параметрів чотириполюсника до якого входить лише опір навантаження має такий вигляд:

.

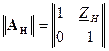Враховуючи , що чотириполюсники сполучені каска дно, їх можна замінити одним еквівалентним чотириполюсником матриця А-параметрів якого дорівнює добутку матриць А-параметрів з’єднаних чотириполюсників

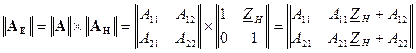. (4.8)

Матричне рівняння для системи А-параметрів в алгебраїчній формі зводиться до системи із двох рівнянь, а саме

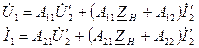. (4.9)

Закоротивши затискачі (тобто у (4.9) покладаємо 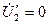), знаходимо вхідний опір

. (4.10)

Вихідний опір чотириполюсника. 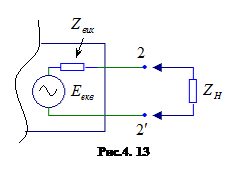Зі сторони вихідних затискачів, до яких приєднуєься опір навантаження, чотириполюсник та генератор можна подати еквівалентним генератором (теорема Тевеніна) з параметрами та . 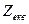(див.рис.4.13). Причому внутрішній опір еквівалентного генератора для навантаження буде відігравати роль вихідного опору чотириполюсника . Очевидно, що в такій ситуації можна отримати формулу для знаходження вихідного опору -

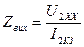, (4.11)

де : 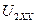- напруга на вихідних затискачах чотириполюсника в режимі холостого ходу ( ), а - струм короткого замикання ( ).

Для знаходження 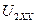та скористаємося системою А-параметрів. Оскільки ,то система А-параметрів в режимі холостого ходу та короткого замикання набувають форм відповідно:

та .

Звідки - , .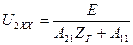

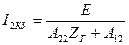Отже

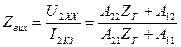. (4.12)

Підійдемо формально і визначимо як вхідний опір чотириполюсника зі сторони затискачів , тобто вхідний опір оберненого чотириполюсника.

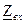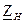Для знаходження вихідного опору лінійна модель чотириполюсника з генератором показана на рис. 4.14. Якщо чотириполюсник та генератор характеризувати В-параметрами, то очевидно, що задача зводиться до задачі знаходження вхідного опору оберненого чотириполюсника , а для знаходження вихідного опору необхідно: А-параметри замінити на В-параметри, на та на :

.

Скориставшись табличними даними перейдемо від В-параметрів до А-параметрів, і отримаємо остаточну формулу для вихідного опору чотириполюсника

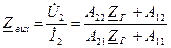. (4.13)

Порівнюючи формули (4.12) та (4.13) робимо висновок: вихідний опір чотириполюсника можемо формально знаходити як вхідний опір оберненого чотириполюсника до вихідних затискачів якого приєднано опір генератора при умові, що усі незалежні джерела усунуті. Аналогічний висновок можна отримати скориставшись іншими системами параметрів.

Знайдемо комплексний коефіцієнт передачі по струму навантаженого чотириполюсника. Для цього в другому рівнянні системи () покладемо 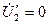. Звідки

. (4.14)

Для знаходження комплексного коефіцієнта передачі по напрузінавантаженого чотириполюсника скористаємося моделлю показаній на рис.4.15. Оскільки два чотириполюсники з’єднані каскадно, то

, (4.15)

де - .

В розгорнутому вигляді рівняння (4.15) для напруги на вході набуває форми

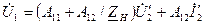. (4.16)

Враховуючи, що при - , з (4.16) заходимо

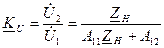(4.17)

Отже частотні характеристики навантаженого чотириполюсника залежать не лише від внутрішньої структури самого чотириполюсника (яка як відомо повністю характеризується відповідними параметрами ) а й від опору навантаження та опору генератора.

Знайдемо вхідні та вихідні опори холостого ходу та короткого замикання:

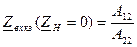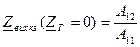, , , . (4.18)

Таким чином опори холостого ходу та короткого замикання є незалежними параметрами які повністю характеризують чотириполюсник.