Энергия гармонических колебаний

В качестве примера рассмотрим механические колебания. Пусть точка совершает гармонические колебания вдоль оси Х, около положения равновесия, принятого за начало координат, по закону

х = Acos(w₀t+j₀)

Кинетическая энергия материальной точки, совершающей гармонические колебания

W_К = 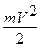= 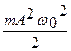sin²(w₀t+j₀) (33)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F:

W_P = - = kx²/2 = 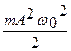cos²(w₀t+j₀) (34)

Полная энергия

W = W_к + W_р =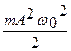

Таким образом, кинетическая и потенциальная энергии гармонических колебаний являются периодическими функциями времени, а полная энергия гармонического осциллятора не зависит от времени и W= (W_к)_max =(W_р)_max .

Пользуясь аналогией, можно получить выражения для энергий магнитного и электрического полей колебательного контура и его полную энергию:

W_маг = 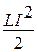= 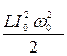sin²(w₀t+j₀) (35)

W_эл= - q²/2С = 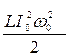cos²(w₀t+j₀) (36)

W = W_маг + W_эл =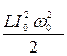

W = (W_маг )_тах =( W_эл )_тах ≠ f (t).