Дифференциальное уравнение затухающих колебаний

Если кроме возвращающей силы на систему действует ещё и сила сопротивления (например, сила трения в механической системе или сопротивление проводника в контуре), то энергия колебательной системы будет расходоваться на преодоление этого сопротивления. Вследствие этого амплитуда колебаний будет уменьшаться и колебания будут затухать. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Рассмотрим затухание на примере пружинного маятника с коэффициентом упругости k,массой m, колеблющегося в среде, например, в жидкости, с коэффициентом сопротивления r. Предположим, что колебания малы и что маятник испытывает вязкое трение. В этом случае можно считать, что сила сопротивления пропорциональна скорости:

F_тр = -r υ = -r 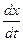, (49)

Знак минус указывает на противоположные напра­вления силы трения и скорости. Закон движения маятника при данных условиях будет иметь вид:

m 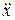= -k x - r 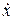. (50)

Преобразуем это выражение:

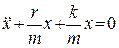(51)

Обозначим: w₀² = 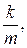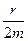= d, где w₀ - циклическая частота собственных колебаний пружинного маятника при отсутствии сил сопротивления, d - коэффициент затухания. Дифференциальное уравнение затухающих коле­баний маятника примет вид:

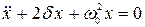(52)

Получили однородное дифференциальное уравнение, второго порядка, описывающее малые затухающие колебания в системе с вязким трением. Его решение имеет вид:

х = A₀ e^{-d t} cos(wt+j) (55)

где ω - частота затухающих колебаний:

w = 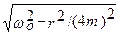. (54)

Уравнение (52) справедливо для любой системы, как механической, так и немеханической, например, для электромагнитного контура. Действительно, для колебательного контура с сопротивлением R второе правило Кирхгофа имеет вид уравнения (29), которое после преобразований принимает вид:

.

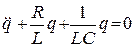Из сравнения с уравнением (52) следует:

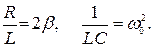
Таким образом, дифференциальное уравнение затухающих колебаний

любой линейной системы в общем виде задается уравнением:

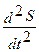+2d 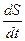+w₀²S = 0. (55)

где S - колеблющаяся величина, описывающая тот или иной физический процесс, d = const – коэффициент затухания, w₀ -собственная циклическая частота колебательной системы, т.е. частота свободных незатуха­ющих колебаний той же колебательной системы (при отсутствии потерь энергии) Решение уравнения (55) имеет вид:

S=A₀e^-dtcos(wt+j)=Acos(wt+j), (56)

где

A = A₀ e^{-d t} (57)

амплитуда затухающих колебаний; A₀ - начальная амплитуда.

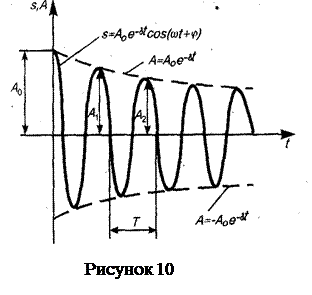Таким образом, затухающие колебания описываются функцией с экспоненциально убывающей амплитудой, т.е. затухающие колебания не являются гармоническими.

Зависимость (56) показана на рисунке 10 сплошной линией, а зависимость (57) — штриховыми линиями. Если пропорциональность силы трения и скорости не выполняются, то и закон убывания амплитуды будет другим. Например при сухом трении F_тр ≠ ƒ(t), F_тр = const и амплитуда убывает согласно геометрической прогрессии. Во многих измерительных приборах наряду с вязким трением (наличие смазки) присутствует и сухое трение (напр. в подшипниках). Пока амплитуды колебаний велики, в затухании доминирует вязкое трение. При малых амплитудах преобладает влияние сухого трения.