Параметры гармонических колебаний
Колебательное движение
Гармонические колебания
Основные понятия
Колебательным движением называются процессы, отличающиеся той или иной степенью повторяемости во времени. Колебания называются периодическими, если параметры, характеризующие состояние системы, повторяются через определенный промежуток времени:
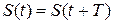 , (1)
, (1)
где 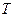 - период колебаний, то есть наименьший промежуток времени, через который повторяется состояние системы, или время одного полного колебания; Ѕ(t) - периодическая функция времени, характеризующая состояние системы - обобщённая координата.
- период колебаний, то есть наименьший промежуток времени, через который повторяется состояние системы, или время одного полного колебания; Ѕ(t) - периодическая функция времени, характеризующая состояние системы - обобщённая координата.
Наиболее важной разновидностью периодических колебаний являются гармонические колебания. Это колебания, происходящие по закону синуса или косинуса:
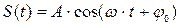 (2)
(2)
Гармоническиеколебаниясовершаются под действием упругой или квазиупругой силы. Упругими называют силы пропорциональные смещению и направленные к положению равновесия, то есть подчиняющееся закону Гука:
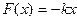 , (3)
, (3)
где 
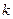 - коэффициент упругости. Квазиупругими являются силы неупругие по своей природе, но действующие так же, как и упругие.
- коэффициент упругости. Квазиупругими являются силы неупругие по своей природе, но действующие так же, как и упругие.
В зависимости от характера внешних воздействий колебания бывают свободные и вынужденные. Свободными являются колебания, возникающие в системе, которая в результате кратковременного внешнего воздействия выведена из положения равновесия и затем предоставлена самой себе. Если колебания такой системы происходят только под действием внутренних сил, которые, как правило, являются упругими или квазиупругими, то такие свободные колебания называются собственными. В реальных условиях свободные колебания носят затухающий характер, так как они происходят при наличии различного вида сил сопротивления.
Системы, совершающие собственные колебания с одной степенью свободы, называются линейными гармоническими осцилляторами. Линейные осцилляторы совершают гармонические колебания лишь при малых отклонениях от положения равновесия. Таким образом, гармонический осциллятор - идеальная модель реальной колеблющейся системы с одной степенью свободы. Примерами гармонического осциллятора являются разные маятники, колебательный контур.
Параметры гармонических колебаний
Пусть гармоническое колебание задано уравнением

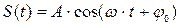 ,
,  (4)
(4)
где А – амплитуда колебаний, представляет собой наибольшее отклонение системы от положения равновесия ( 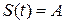 при
при 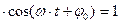 );
); 
φ- фаза колебаний, физическая величина, однозначно характеризующая состояния гармонического осциллятора в данный момент времени;
j 0 – начальная фаза колебаний ( при t = 0 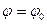 );
);
w - циклическая частота собственных гармонических колебаний;
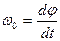 , т.е. циклическая частота является скоростью изменения фазы колебаний;
, т.е. циклическая частота является скоростью изменения фазы колебаний;
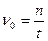 - линейная частота колебаний; она определяет число колебаний в единицу времени. Линейная частота связана с циклической частотой соотношением:
- линейная частота колебаний; она определяет число колебаний в единицу времени. Линейная частота связана с циклической частотой соотношением: 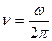 .
.
Т- период колебаний, определяет время одного колебания
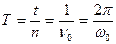 ; (5)
; (5)
Dj - разность фаз или сдвиг по фазе. Если 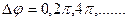 , то колебания
, то колебания
происходят в одинаковой фазе, 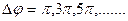 - в противофазе.
- в противофазе.
Дата добавления: 2015-07-18; просмотров: 2613;
