Поверхности второго порядка. Вспомним, что плоскость задается в пространстве уравнением первой степени: , поэтому плоскость называется поверхностью первого порядка.
Вспомним, что плоскость задается в пространстве уравнением первой степени: 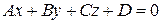 , поэтому плоскость называется поверхностью первого порядка.
, поэтому плоскость называется поверхностью первого порядка.
Поверхность, задаваемая уравнением второй степени (по совокупности) с тремя текущими координатами, называется поверхностью второго порядка. Известно, что существуют следующие поверхности 2-го порядка (за исключением вырожденных случаев):
1. сфера;
2. эллипсоид;
3. гиперболоид (одно- и двуполостный);
4. параболоид (эллиптический и гиперболический);
5. конус;
6. цилиндрические поверхности 2-го порядка.
Приведем их канонические уравнения.
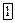 Сфера Сфера 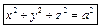

|   Эллипсоид Эллипсоид 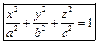
|
  Однополостный гиперболоид Однополостный гиперболоид 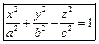
|   Двуполостный гиперболоид Двуполостный гиперболоид 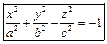 . .
|
 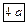 Эллиптический параболоид Эллиптический параболоид  . .
|   Гиперболический параболоид Гиперболический параболоид 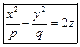 (p>0, q>0).
(p>0, q>0).
|
 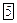 Эллиптический конус: Эллиптический конус:
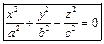
|  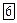 Цилиндрическая поверхность — поверхность, образуемая движением прямой Цилиндрическая поверхность — поверхность, образуемая движением прямой 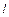 (в каждом своём положении называемой образующей) вдоль кривой (в каждом своём положении называемой образующей) вдоль кривой 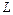 (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению. (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
 (В каноническом уравнении отсутствует одна из переменных)
Пример: (В каноническом уравнении отсутствует одна из переменных)
Пример:
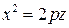 - параболический цилиндр
- параболический цилиндр
|
Дата добавления: 2015-07-18; просмотров: 668;
