Кривые второго порядка
Линии, определяемые уравнениями второй степени с двумя текущими координатами

называются кривыми второго порядка. Это уравнение на плоскости (если не считать случаев вырождения и распадения) определяет окружность, эллипс, гиперболу, параболу.
Окружность – множество точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой ее центром. Расстояние от точки окружности до центра называется радиусом окружности.
Напомним, уравнение окружности радиуса 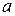 с центром в точке
с центром в точке 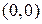 имеет вид
имеет вид
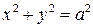 ,
,
уравнение окружности радиуса 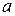 с центром в точке
с центром в точке 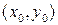 :
:
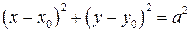 .
.
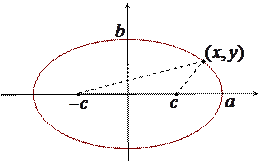 Рис Эллипс– множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Рис Эллипс– множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через 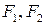 , расстояние между ними через
, расстояние между ними через 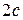 , сумму расстояний от произвольной точки эллипса до фокусов через
, сумму расстояний от произвольной точки эллипса до фокусов через 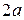 . По определению
. По определению 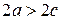 . Выберем ДСК так, чтобы фокусы лежали на оси
. Выберем ДСК так, чтобы фокусы лежали на оси 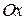 , а начало координат совпадало с серединой отрезка
, а начало координат совпадало с серединой отрезка 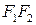 . Тогда фокусы имеют координаты
. Тогда фокусы имеют координаты 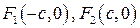 . Пусть
. Пусть 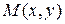 – произвольная точка эллипса. По определению имеем
– произвольная точка эллипса. По определению имеем 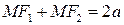 , т.е.
, т.е.
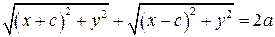 .
.
Отсюда
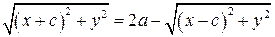 .
.
Возведем обе части в квадрат, а затем уединим корень:
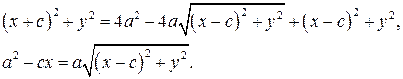
Возведем еще раз в квадрат и перегруппируем:
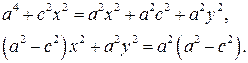
Обозначив 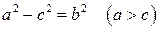 , получим
, получим

– каноническое уравнение эллипса.
 Числа
Числа 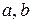 называются полуосями эллипса. Степень «вытянутости» эллипса характеризует эксцентриситет
называются полуосями эллипса. Степень «вытянутости» эллипса характеризует эксцентриситет
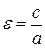 .
.
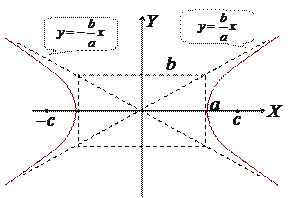
Рис Гипербола– множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через 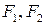 , расстояние между ними через
, расстояние между ними через 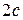 , модуль разности расстояний от произвольной точки гиперболы до фокусов через
, модуль разности расстояний от произвольной точки гиперболы до фокусов через 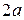 . По определению
. По определению  . Выберем ДСК так, чтобы фокусы лежали на оси
. Выберем ДСК так, чтобы фокусы лежали на оси 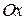 , а начало координат совпадало с серединой отрезка
, а начало координат совпадало с серединой отрезка 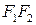 .
.
Докажите самостоятельно, что уравнение гиперболы в этом случае имеет вид
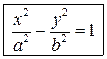 ,
,
где обозначено 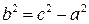 .
.
Здесь 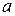 – действительная,
– действительная, 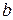 – мнимая полуоси гиперболы, прямые
– мнимая полуоси гиперболы, прямые 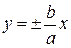 называются асимптотами. Эксцентриситет
называются асимптотами. Эксцентриситет 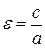 .
.
Парабола– множество точек плоскости, каждая из которых одинаково удалена от данной точки 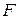 , называемой фокусом, и данной прямой
, называемой фокусом, и данной прямой 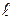 , называемой директрисой. Расстояние
, называемой директрисой. Расстояние  от фокуса до директрисы называется параметром параболы.
от фокуса до директрисы называется параметром параболы.
Выберем ДСК как указано на рисунке. Тогда уравнение параболы имеет вид:
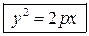 .
.
 3. 1. Привести к каноническому виду уравнение
3. 1. Привести к каноническому виду уравнение 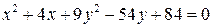 и построить кривую.
и построить кривую.
Решение. Т.к. 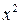 и
и 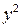 входят в уравнение с одинаковыми знаками, но разными коэффициентами, то оно описывает эллипс. Сгруппируем слагаемые следующим образом
входят в уравнение с одинаковыми знаками, но разными коэффициентами, то оно описывает эллипс. Сгруппируем слагаемые следующим образом
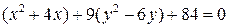
и, используя известную формулу выделения полного квадрата 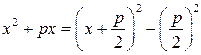 , выделим в выражениях в скобках полные квадраты:
, выделим в выражениях в скобках полные квадраты:
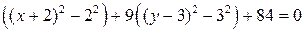 .
.
После преобразований, получим:
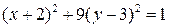 или
или 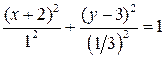 .
.
Это уравнение эллипса с центром в точке 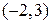 и полуосями
и полуосями 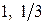 . рис
. рис
3. 2. Привести к каноническому виду уравнение 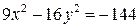 , построить кривую, найти координаты фокусов. рис
, построить кривую, найти координаты фокусов. рис
Решение. Разделив обе части уравнения на (-144), получим
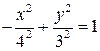 .
.
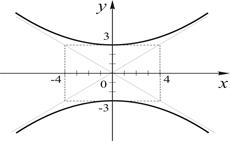 Очевидно, это уравнение гиперболы, однако переменные
Очевидно, это уравнение гиперболы, однако переменные 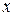 и
и 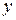 «поменялись ролями» – коэффициент при
«поменялись ролями» – коэффициент при 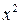 равен (-1), что следует учесть при построении линии: фокусы этой гиперболы расположены на оси
равен (-1), что следует учесть при построении линии: фокусы этой гиперболы расположены на оси 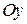 . Чтобы найти их координаты, воспользуемся равенством
. Чтобы найти их координаты, воспользуемся равенством 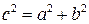 . Откуда
. Откуда 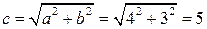 , т.е.
, т.е. 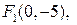
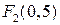 .
.
 3. 3. Найти проекцию фокуса параболы
3. 3. Найти проекцию фокуса параболы 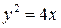 на прямую
на прямую 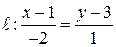 .
.
Решение. Рис Из уравнения параболы имеем: 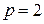 , т.е. координаты фокуса
, т.е. координаты фокуса 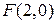 . Проекция
. Проекция 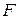 на
на 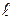 – точка пересечения
– точка пересечения 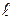 и прямой, проведенной из
и прямой, проведенной из 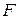 перпендикулярно
перпендикулярно 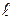 (обозначим ее
(обозначим ее  ). Уравнение
). Уравнение 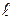 представлено в каноническом виде, числа
представлено в каноническом виде, числа 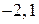 являются координатами вектора, направляющего прямую, он же является нормалью к прямой
являются координатами вектора, направляющего прямую, он же является нормалью к прямой  . Используя уравнение прямой по точке
. Используя уравнение прямой по точке 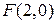 и нормали
и нормали 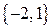 (см…), получим:
(см…), получим: 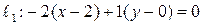 или
или
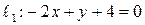 .
.
Координаты искомой точки 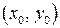 пересечения прямых
пересечения прямых 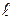 и
и  должны удовлетворять их уравнениям, т.е.
должны удовлетворять их уравнениям, т.е. 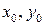 – решение системы
– решение системы
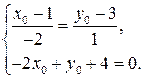
Первое уравнение преобразуется на основании свойства пропорции (произведение средних членов равно произведению крайних) к виду 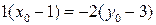 или
или 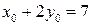 . Решим полученную систему уравнений
. Решим полученную систему уравнений
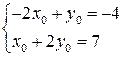 ,
,
например, по формулам Крамера: 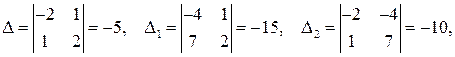
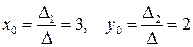 .
.
Ответ: 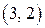
Уравнение поверхности и линии в пространстве
Пусть задана ДСК в пространстве. Уравнением поверхности называется такое уравнение 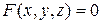 с тремя переменными, которому удовлетворяют координаты каждой точки данной поверхности и не удовлетворяют координаты любой другой точки. Переменные
с тремя переменными, которому удовлетворяют координаты каждой точки данной поверхности и не удовлетворяют координаты любой другой точки. Переменные 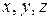 называются текущими координатами точек поверхности.
называются текущими координатами точек поверхности.
Линию в пространстве можно рассматривать как линию пересечения поверхностей: 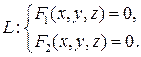
Плоскостьописывается общим уравнением вида
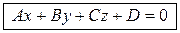 ,
,
где хотя бы один из коэффициентов 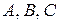 отличен от нуля.
отличен от нуля.

 3. 4. Дано: точка
3. 4. Дано: точка 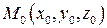 , вектор
, вектор 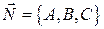 .
.
Найти: уравнение плоскости, проходящей через точку 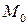 перпендикулярно вектору
перпендикулярно вектору 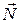 .
.
Решение. Выберем на плоскости произвольно точку 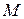 с текущими координатами
с текущими координатами 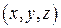 . Тогда вектор
. Тогда вектор 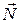 перпендикулярен вектору
перпендикулярен вектору 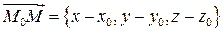 . Т.е.
. Т.е. 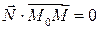 . Получим
. Получим
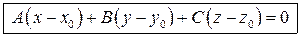
– уравнение плоскости по точке и нормали (любой ненулевой вектор, перпендикулярный плоскости, будем называть нормалью).
Приведем без доказательства еще два вида уравнений плоскости.
 Уравнение плоскости, проходящей через точки
Уравнение плоскости, проходящей через точки 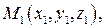
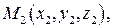
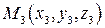 (не лежащие на одной прямой):
(не лежащие на одной прямой):
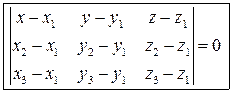 .
.
Уравнение плоскости, отсекающей на осях координат ненулевые «отрезки» 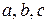 .
.

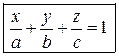 .
.
Дата добавления: 2015-07-18; просмотров: 1235;
