Пространство .
Последовательность 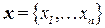 из
из 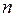 действительных чисел, расположенных в определенном порядке, называется
действительных чисел, расположенных в определенном порядке, называется 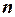 -мерным вектором. Совокупность всех
-мерным вектором. Совокупность всех 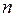 -мерных векторов
-мерных векторов 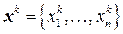 (
( 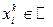 ) обозначим
) обозначим  . Введем в
. Введем в  операции сложения и умножения на вещественное число поэлементно:
операции сложения и умножения на вещественное число поэлементно: 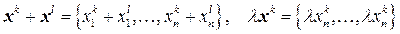 ,
,
нуль-вектором назовем вектор, все координаты которого равны нулю: 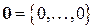 .
.
Множество, на котором введены операции сложения и умножения на число, удовлетворяющие обычным свойствам арифметических действий, называется линейным пространством. Таким образом, множество  с введенными выше операциями является линейным пространством.
с введенными выше операциями является линейным пространством.
Совокупность из 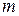 векторов пространства
векторов пространства  будем называть линейно независимой, если их линейная комбинация
будем называть линейно независимой, если их линейная комбинация
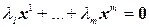 (*)
(*)
лишь при условии 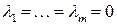 . В противном случае, т.е. если существуют такие числа
. В противном случае, т.е. если существуют такие числа 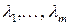 не все равные нулю, что выполняется равенство (*), совокупность
не все равные нулю, что выполняется равенство (*), совокупность 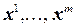 назовем линейно зависимой.
назовем линейно зависимой.
Так, например, векторы 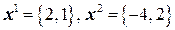 в пространстве
в пространстве 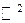 являются линейно зависимыми, т.к. существует их нетривиальная (не все
являются линейно зависимыми, т.к. существует их нетривиальная (не все 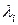 равны нулю) линейная комбинация, равная нуль-вектору:
равны нулю) линейная комбинация, равная нуль-вектору: 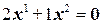 .
.
Обозначим 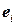 – вектор из
– вектор из  , все координаты которого равны нулю, за исключением
, все координаты которого равны нулю, за исключением 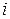 - ой, которая равна
- ой, которая равна 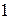 :
:
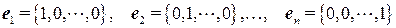 .
.
Эта система векторов линейно независима, и любой вектор 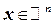 единственным образом можно представить в виде линейной комбинации этих векторов:
единственным образом можно представить в виде линейной комбинации этих векторов:
.
Любая система 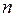 векторов, обладающих такими свойствами, называется базисом пространства
векторов, обладающих такими свойствами, называется базисом пространства  .
.
В случаях 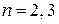 вектор
вектор  можно рассматривать как вектор, заданный своими проекциями на оси координат. Тогда в «привычных» обозначениях: система
можно рассматривать как вектор, заданный своими проекциями на оси координат. Тогда в «привычных» обозначениях: система 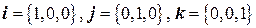 является базисом в пространстве
является базисом в пространстве 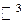 , а
, а 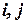 – в
– в 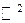 .
.
В  существует бесконечное множество базисов. В частности, в
существует бесконечное множество базисов. В частности, в 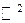 – это любая пара неколлинеарных, а в
– это любая пара неколлинеарных, а в 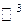 – любая тройка некомпланарных векторов.
– любая тройка некомпланарных векторов.
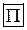 Покажем, что векторы
Покажем, что векторы 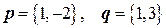 образуют базис в
образуют базис в 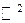 , и найдем разложение вектора
, и найдем разложение вектора 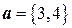 по базису
по базису 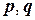
1. Составим линейную комбинацию 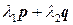 . Выясним условия на
. Выясним условия на 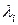 , при которых эта комбинация дает
, при которых эта комбинация дает 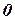 .
.
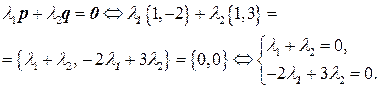
Определитель полученной однородной системы 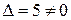 , значит (см. замечание к теме «СЛАУ») она имеет только тривиальное решение
, значит (см. замечание к теме «СЛАУ») она имеет только тривиальное решение 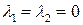 .
.
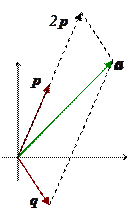
2. Найдем координаты вектора в этом базисе: 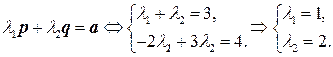 .
.
Ответ: 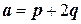 . (На рис результат проиллюстрирован геометрически.)
. (На рис результат проиллюстрирован геометрически.)
Дата добавления: 2015-07-18; просмотров: 648;
