Замечания.
- Если в уравнении плоскости свободный член 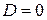 , то плоскость проходит через начало координат.
, то плоскость проходит через начало координат.
- Если в уравнении отсутствует какая-либо координата, то плоскость проходит параллельно соответствующей оси.
- Коэффициенты при 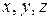 в общем уравнении – координаты нормали плоскости
в общем уравнении – координаты нормали плоскости 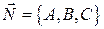 .
.
- Уравнения координатных плоскостей 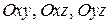 имеют вид
имеют вид 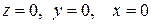 соответственно.
соответственно.
 Построить плоскость по ее уравнению
Построить плоскость по ее уравнению
1. 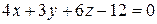 .
Все коэффициенты в уравнении отличны от нуля, поэтому удобно преобразовать его к уравнению в отрезках: .
Все коэффициенты в уравнении отличны от нуля, поэтому удобно преобразовать его к уравнению в отрезках:
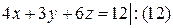
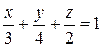 . .
| 
|
2. 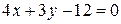 .
Уравнение не содержит переменную .
Уравнение не содержит переменную 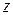 , значит, плоскость параллельна оси , значит, плоскость параллельна оси 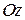 , и ее направляющей служит прямая , и ее направляющей служит прямая 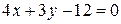 . .
| 
|
3. 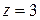 .
Это плоскость, параллельная осям .
Это плоскость, параллельная осям  и и 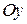 , иначе говоря, параллельная плоскости , иначе говоря, параллельная плоскости 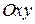 , проходящая «на высоте 3». , проходящая «на высоте 3».
| 
|
Прямая в пространствезадается каноническим, параметрическим или общим уравнениями.
 1. Найдем уравнение прямой, проходящей через заданную точку
1. Найдем уравнение прямой, проходящей через заданную точку 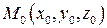 параллельно заданному вектору
параллельно заданному вектору 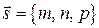 .
.
Выберем на прямой произвольно точку 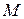 с текущими координатами
с текущими координатами 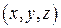 . Тогда вектор
. Тогда вектор 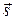 параллелен вектору
параллелен вектору 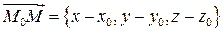 :
:

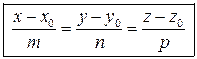 .
.
Это уравнение называется каноническимуравнением прямой в пространстве.
1а. Рассуждая аналогично, получим уравнение прямой по двум ее точкам 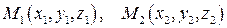 :
:
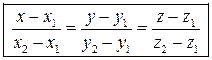 .
.
2. Введем в каноническом уравнении параметр 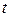 :
:
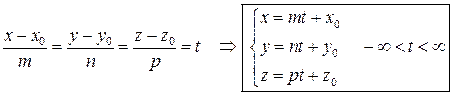 .
.
Уравнение прямой в таком виде называется параметрическим. При фиксированном значении параметра получаем соответствующую точку прямой. Придавая 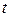 все значения из числового промежутка
все значения из числового промежутка 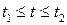 , получим соответствующий отрезок прямой.
, получим соответствующий отрезок прямой.
 3. Также прямую можно задать как линию пересечения непараллельных плоскостей.
3. Также прямую можно задать как линию пересечения непараллельных плоскостей.
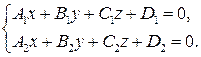
Такое уравнение называется общим.Почему «альфа»???
Для решения задач, необходимо уметь переходить от одной формы записи прямой к другой.

 Найти расстояние от точки
Найти расстояние от точки 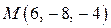 до прямой
до прямой 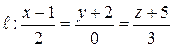 .рис. Не такой!!!
.рис. Не такой!!!
Решение. Убедимся, что 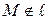 . Подставив ее координаты в уравнение прямой, мы видим:
. Подставив ее координаты в уравнение прямой, мы видим: 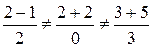 (если хотя бы одно из равенств не выполнено, то точка не принадлежит прямой). Обозначим
(если хотя бы одно из равенств не выполнено, то точка не принадлежит прямой). Обозначим 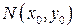 – проекция
– проекция 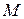 на
на 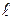 . Тогда расстояние от
. Тогда расстояние от 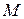 до
до 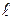
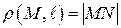 .
.
Точку 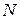 найдем как пересечение заданной прямой
найдем как пересечение заданной прямой 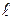 и перпендикулярной к ней плоскости
и перпендикулярной к ней плоскости 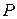 , проходящей через
, проходящей через 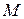 . Из рисунка видно, что вектор
. Из рисунка видно, что вектор 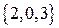 , направляющий прямую, является для
, направляющий прямую, является для 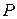 нормалью, т.е. можно воспользоваться уравнением плоскости по точке и нормали:
нормалью, т.е. можно воспользоваться уравнением плоскости по точке и нормали:
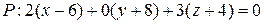 .
.
Тогда 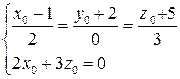 .
.
Чтобы решить систему, предварительно приведем уравнение прямой к параметрическому виду:
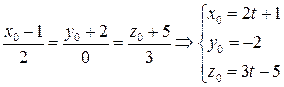
И затем решим ее методом подстановки.
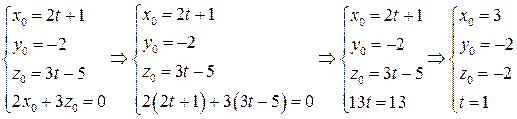
Таким образом 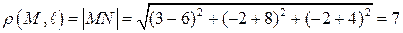 .
.
Дата добавления: 2015-07-18; просмотров: 648;
