Практические приемы отыскания уравнения прямой

	название	рисунок	уравнение
1.	По точке и нормальному вектору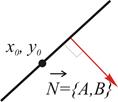
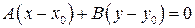
2.	По точке и направляющему вектору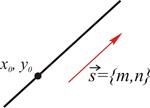
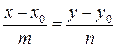
3.	По точке и угловому коэффициенту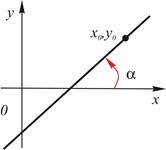
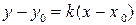
4.	По двум точкам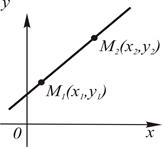
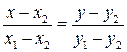
5. ю	В отрезках на осях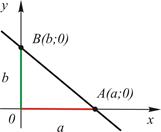
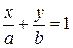
6.	Вертикаль
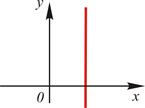
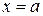
7.	Горизонталь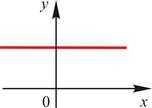

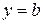
Приведем выводы первых двух уравнений.

1. Выберем произвольно точку с текущими координатами 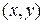на прямой. Тогда вектор 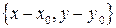перпендикулярен заданному вектору 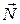. По условию перпендикулярности (см. приложение 2а скалярного произведения) имеем:

,

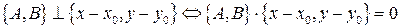т.е. .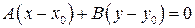

Далее любой перпендикулярный прямой вектор будем называть нормалью прямой.

Полученное уравнение можно записать в общем виде 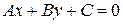, где обозначено .

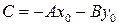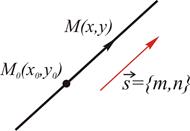
2. Выберем произвольно точку с текущими координатами 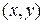на прямой. Тогда вектор 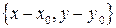коллинеарен заданному вектору (см. замечание к теореме о соответствии мд. в-рами и их коорд-ми при линейных операциях), т.е. их координаты должны быть пропорциональны:

.

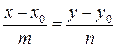Далее любой параллельный прямой вектор будем называть направляющимпрямую вектором, уравнение вида 2 – каноническим уравнением прямой.