Раздел 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Уравнение линии на плоскости
Пусть задана ДСК на плоскости. Уравнением линии на плоскости называется такое уравнение 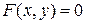 с двумя переменными, которому удовлетворяют координаты
с двумя переменными, которому удовлетворяют координаты 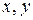 каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Переменные
каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Переменные 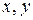 в уравнении линии называются текущими координатами точек линии.
в уравнении линии называются текущими координатами точек линии.
Пример 1.1. Доказать, что уравнение окружности радиуса 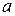 с центром в начале координат имеет вид
с центром в начале координат имеет вид
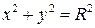 . (*)
. (*)
Решение. Рассмотрим 3 случая
а) точка 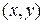 лежит на окружности. Тогда по теореме Пифагора получаем:
лежит на окружности. Тогда по теореме Пифагора получаем: 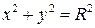 .
.
б) точка 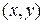 – вне круга. Тогда
– вне круга. Тогда 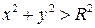 .
.
в) точка 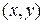 – внутри круга. Тогда
– внутри круга. Тогда 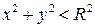 .
.
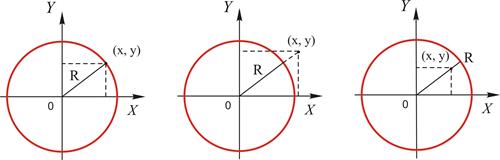
| ||
| а) | б) | в) |
 Равенство (*) выполняется для всех точек окружности и не выполняется для других точек плоскости. Т.о. (*) – искомое уравнение.
Равенство (*) выполняется для всех точек окружности и не выполняется для других точек плоскости. Т.о. (*) – искомое уравнение.
Уравнение линии зависит от выбора системы координат. Например, уравнение окружности радиуса 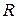 с центром в точке
с центром в точке 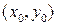 имеет вид
имеет вид
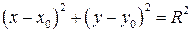
Дата добавления: 2015-07-18; просмотров: 885;
