Граничні теореми у схемі Бернуллі
Для наближеного обчислення ймовірності появи події А у n незалежних випробуваннях m разів схеми Бернуллі при великих n і малих р таких, що nр < 10, доцільно використовувати формулу Пуассона:
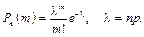
Приклад 9. Підручник надруковано тиражем 90000 примірників. Імовірність неправильного брошурування підручника дорівнює 0,0001. Знайти ймовірність того, що тираж має 5 бракованих підручників.
Розв’язання. Брошурування підручника можна розглядати як випробування, що вкладається в схему Бернуллі. Кількість випробувань n велика, а ймовірність кожного випробування р незначна. Тому в цьому разі доцільно застосувати формулу Пуассона. Згідно з умовою задачі маємо
n = 90000, р = 0,0001.
Отже, при l = np = 9 маємо
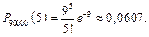 ·
·
Локальна теорема Муавра — Лапласа. Якщо у схемі Бернуллі кількість випробувань n достатньо велика, а ймовірність р появи події А в усіх випробуваннях однакова та відмінна від нуля й одиниці, то ймовірність появи m разів події А можна знайти наближено за формулою
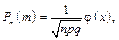
де 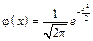 — функція Гаусса,
— функція Гаусса, 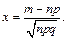
Інтегральна теорема Муавра — Лапласа. Якщо у схемі Бернуллі кількість випробувань n достатньо велика, а ймовірність р появи події А в усіх випробуваннях однакова та відмінна від нуля й одиниці, то ймовірність появи події A не менше m1 і не більше m2 разів можна знайти за наближеною формулою
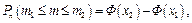
де 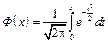 — інтегральна функція Лапласа,
— інтегральна функція Лапласа, 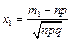 ,
, 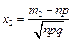 .
.
Зазначимо, що для функцій Гаусса та Лапласа складені спеціальні таблиці (див. додаток).
Приклад 10. Відомо, що 30 лампочок зі 100 на даному виробництві є бракованими. Партія лампочок у кількості 500 штук була одержана магазином для реалізації. Знайти ймовірність того, що з них бракованими виявиться:
а) 155 штук;
б) не менше 100 і не більше 200 штук.
Розв’язання. Оскільки n = 500 є достатньо великим числом, то використовувати формулу Бернуллі нераціонально. Зазначимо, що в даній задачі має місце схема Бернуллі, оскільки випуск бракованої лампочки (ймовірність дорівнює 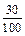 ) не залежить від того, чи були бракованими попередні.
) не залежить від того, чи були бракованими попередні.
а)Оскільки m = 155, то використаємо локальну формулу Муавра — Лапласа 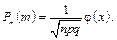
У нашому випадку 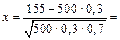 0,49, j(0,49) = 0,3538. Отже,
0,49, j(0,49) = 0,3538. Отже, 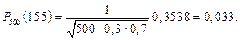
б) Оскільки 100 £ m £ 200, то використаємо інтегральну формулу Лапласа 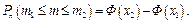
У нашому випадку 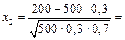 4,88,
4,88, 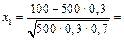 –4,88. Оскільки функція Лапласа є непарною, тобто Ф(–x) = –Ф(х), то Ф(–4,88) =
–4,88. Оскільки функція Лапласа є непарною, тобто Ф(–x) = –Ф(х), то Ф(–4,88) =
= –Ф(4,88) = 0,4999.
Отже, 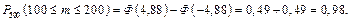 ·
·
Теорема Бернуллі. Якщо в n незалежних випробуваннях імовірність р появи події А однакова й подія А відбудеться m разів, то для будь-якого додатного числа e > 0 виконується рівність
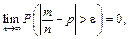
тобто подія, для якої відхилення визначається формулою
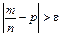
при великих значеннях n майже неможлива. Тому протилежна подія
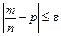
майже достовірна:
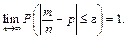
Дану формулу можна записати так:
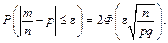
Ці формули доцільно застосовувати за умови n > 100, npq > 20.
Приклад 11. Імовірність появи події в кожному із 625 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що відносна частота появи події відхиляється від імовірності за абсолютною величиною не більше ніж на 0,04.
Розв’язання. За умовою задачі
n = 625; p = 0,8; q = 0,2; e = 0,04.
Потрібно знайти 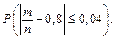
За теоремою Бернуллі маємо
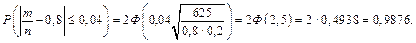 ·
·
Приклад 12. Імовірність появи деякої події в кожному з незалежних випробувань дорівнює 0,5. Знайти кількість випробувань n, при якій з імовірністю 0,7698 можна очікувати, що відносна частота появи події відхилиться від її ймовірності за абсолютною величиною не більше ніж на 0,02.
Розв’язання. За умовою задачі
р = 0,5; q = 0,5; e = 0,02.
Потрібно знайти кількість випробувань n, для якої
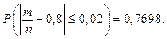
За теоремою Бернуллі маємо
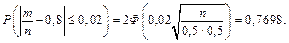
Звідси
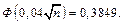
Визначивши за додатком аргумент інтегральної функції Лапласа, при якому ця функція дорівнює 0,3849, отримаємо рівняння
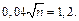
Отже,
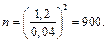 ·
·
Дата добавления: 2015-08-26; просмотров: 3063;
