Закон великих чисел
За певних умов сумарна поведінка великої кількості випадкових величин є передбачуваною. Це випливає з теорем, які носять загальну назву — закон великих чисел.
Закони великих чисел описують стійкість середніх значень масових випадкових явищ. Історично першим законом великих чисел була теорема Бернуллі.
Теорема Бернуллі. Нехай m — кількість появ події А в серії n незалежних випробовувань, у кожному з яких подія А відбувається з імовірністю p. Тоді для довільного e > 0 справджується рівність
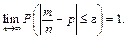
Лема Чебишева. Якщо всі можливі значення випадкової величини X є невід’ємними, тоді ймовірність того, що вона при випробовуванні набере значення, більшого від певного додатного числа b, не більше від дробу 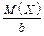 :
:
P(X > b) £ 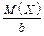 .
.
Нерівність Чебишева. Імовірність того, що відхилення випадкової величини X від її математичного сподівання за абсолютною величиною не перевищить деяке число e > 0, не менше від:
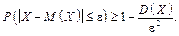
Теорема Чебишева. Нехай Xi — попарно незалежні випадкові величини, рівномірно обмежені за дисперсіями (D(Xi) £ C, i = 1, 2, ..., n). Тоді для довільного e > 0
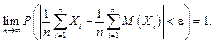
Проте зручніше записати дану теорему у вигляді
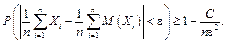
Центральна гранична теорема Ляпунова. Якщо Xi, i = 1, 2, ..., n — попарно незалежні однаково розподілені випадкові величини з математичним сподіванням M(Xi) = а і D(Xi) = s2, то за великого n розподіл суми X1 + X2 + ... + Xn = X близький до нормального закону.
Як наслідок зі сказаного вище, можна отримати формулу, яка має велике практичне застосування:
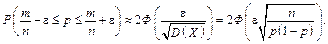
Приклад 17. Використовуючи нерівність Чебишева, знайти ймовірність події А, яка полягає в тому, що випадкова величина X набуде значення, яке відрізнятиметься від математичного сподівання М(Х) на величину, що не перевищує потроєного середнього квадратичного відхилення. Чи зміниться відповідь, якщо відомо, що випадкова величина X має нормальний розподіл?
Розв’язання. За нерівністю Чебишева
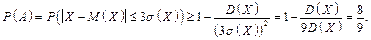
Отже,
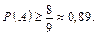
Якщо X має нормальний розподіл (див. приклад 15), то
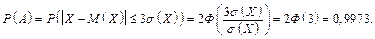 ·
·
Приклад 18. При виробництві дискет брак становить 1%. Скільки дискет потрібно відібрати для перевірки якості, щоб з імовірністю 0,95 можна було стверджувати, що у випадковій вибірці дискет відсоток бракованих відрізняється від 1% не більш як на 0,5%?
Розв’язання. Кількість бракованих дискет є випадковою величиною
X = X1 + X2 + ... + Xn,
де X1, X2, ..., Xn — незалежні однаково розподілені випадкові величини; Xi — випадкова величина, яка дорівнює кількості бракованих дискет при виготовленні однієї дискети, тобто Xi може набувати значення або 0, або 1 з імовірністю відповідно 0,99 і 0,01. Якщо n — досить велике число, то за центральною граничною теоремою розподіл випадкової величини X близький до нормального. Тому
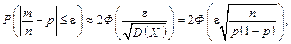
де 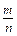 — частота браку; р = 0,01; e = 0,005; n — невідома кількість дискет. Число n потрібно вибрати таким, щоб
— частота браку; р = 0,01; e = 0,005; n — невідома кількість дискет. Число n потрібно вибрати таким, щоб
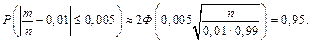
Іншими словами,
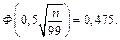
За таблицею значень функції Лапласа (дод. 2) знаходимо значення аргументу х таке, що Ф(х) = 0,475:
х = 1,96.
Розв’язавши рівняння 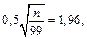 отримаємо:
отримаємо: 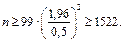 ·
·
Дата добавления: 2015-08-26; просмотров: 1391;
