Елементи математичної статистики. Вибірковий метод
Нехай для вивчення кількісної (дискретної чи неперервної) ознаки X із генеральної сукупності отримано вибірку x1, x2, ... , хn обсягом n.
Якщо записати елементи вибірки в порядку зростання, отримаємо варіаційний ряд.
Спостережувані різні значення xі ознаки X називають варіантами, кількість значень однієї варіанти у вибірці — її частотою nі (сума частот усіх варіант дорівнює обсягу вибірки), відношення частоти до обсягу вибірки — відносною частотою або емпіричною ймовірністю 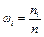 (сума відносних частот усіх варіант дорівнює одиниці).
(сума відносних частот усіх варіант дорівнює одиниці).
Статистичним розподілом вибірки називають перелік варіант варіаційного ряду з відповідними їм частотами і/або відносними частотами. Статистичний розподіл також задають у вигляді послідовності замкнених справа напівінтервалів і відповідних їм частот і/або відносних частот (частотою інтервалу вважають суму частот усіх варіант з даного інтервалу).
Щоб підкреслити зазначені відмінності в першому випадку говорять про точковий, а в другому — про інтервальний статистичний розподіл вибірки.
Приклад 1. Під час дослідження кількісної ознаки X із генеральної сукупності було отримано вибірку
4, 3, 6, 4, 7, 2, 5, 1, 2, 5, 4, 4, 3, 5, 6, 3, 4, 1, 3, 4.
Знайти обсяг вибірки, побудувати варіаційний ряд вибірки та її статистичний розподіл.
Розв’язання. Оскільки вибірка складається з 20 значень, то обсяг вибірки n = 20.
Побудуємо варіаційний ряд вибірки:
1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7.
У даній вибірці всього сім різних значень, тобто варіант:
1, 2, 3, 4, 5, 6, 7.
Знайдемо їх частоти:
n1 =2; n2 = 2; n3 = 4; n4 = 6; n5 = 3; n6 = 2; n7 = 1.
Запишемо шуканий статистичний розподіл:
| xi | ||||||||
| ni | · |
Емпіричною функцією розподілу називають функцію
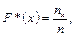
де nх — кількість елементів вибірки, менших від х (тобто сума частот усіх варіант, менших від х); n — обсяг вибірки.
Емпірична функція розподілу має такі властивості.
Властивість 1. Емпірична функція розподілу F*(х) невід’ємна і не перевищує одиниці при будь-яких значеннях х:
F*(х)Î[0; 1].
Властивість 2. Емпірична функція розподілу F*(х) неспадна:
х < у Þ F*(х) £ F*(у).
Властивість 3. Якщо х1 — найменша варіанта, а хn — найбільша, то емпірична функція розподілу F*(х) = 0 при х £ x1 і F*(х) = 1 при х > хn.
Приклад 2. Знайти емпіричну функцію розподілу за даним розподілом вибірки:
| xi | |||||
| ni |
Розв’язання. Знайдемо обсяг вибірки:
n = 2 + 4 + 7 + 4 + 3 = 20.
Оскільки найменша варіанта дорівнює трьом,
F*(x) = 0,
якщо х £ 3.
Значення X < 5, а саме значення х1 = 3 спостерігалося двічі, тому
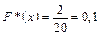 ,
,
якщо 3 < x £ 5.
Значення X < 7, а саме х1 = 3 і x2 = 5 спостерігалися 2 + 4 = 6 разів, тому
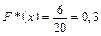 ,
,
якщо 5 < х £ 7.
Значення X < 10, а саме х1 = 3, x2 = 5 і x3 = 7 спостерігалися 2 + 4 + 7 = 13 разів, тому
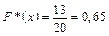 ,
,
якщо 7 < х £ 10.
Значення X < 15, а саме х1 = 3, x2 = 5, x3 = 7 і x4 = 10 спостерігалися 2 + 4 +
+ 7 + 4 = 17 разів, тому
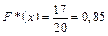 ,
,
якщо 10 < x £ 15.
Оскільки x5 = 15 — найбільша варіанта, то
F*(х) = 1
якщо х > 15.
Отже, запишемо шукану емпіричну функцію:
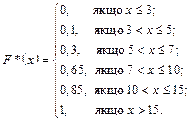
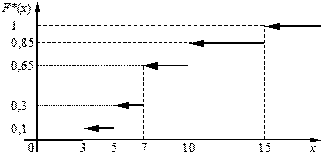
Графік цієї функції зображено на рис. 1.
 ·
·
Рис. 1
Полігоном частот називають ламану, відрізки якої з’єднують точки
(х1, n1), (х2, n2), ..., (хk, nk),
де xі — варіанти вибірки; ni — відповідні частоти, і = 1, 2, ... .
Полігоном відносних частот називають ламану, відрізки якої з’єднують точки
(х1, w1), (х2, w2), ..., (хk, wk).
де xі — варіанти вибірки; wi — відповідні емпіричні ймовірності, і = 1, 2, ... .
Гістограмою частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є частинні інтервали довжиною D, а висоти дорівнюють відношенню 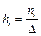 (густина, щільність частоти). Площа і-го частинного прямокутника
(густина, щільність частоти). Площа і-го частинного прямокутника
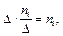
тобто сумі частот варіант, що потрапили в i-й частинний інтервал. Площа гістограми частот дорівнює сумі всіх частот, тобто обсягу вибірки n.
Гістограмою відносних частот називають ступінчасту фігуру, що складається з прямокутників, основами яких є частинні інтервали довжиною D, а висоти дорівнюють відношенню 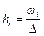 (густина, щільність відносної частоти). Площа i-го частинного прямокутника
(густина, щільність відносної частоти). Площа i-го частинного прямокутника
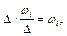
тобто сумі відносних частот варіант, що потрапили в i-й інтервал. Площа гістограми відносних частот дорівнює сумі всіх відносних частот, тобто одиниці.
Приклад 3. Побудувати полігон і гістограму частот за даним розподілом вибірки:
| хi | |||||||
| ni |
Розв’язання. Відкладемо на осі абсцис значення варіант xi, а на осі ординат — значення відповідних їм частот ni. Послідовно з’єднуючи між собою точки (xi; ni) відрізками, отримуємо полігон частот (рис. 2).
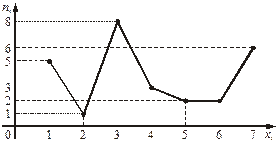
Рис. 2
Побудуємо гістограму для даного прикладу. Для цього знайдемо довжину інтервалу D: 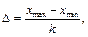 де k — кількість прямокутників (вибирають довільним чином).
де k — кількість прямокутників (вибирають довільним чином).
Нехай k = 4, тоді 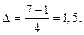
Тоді висоти відповідних прямокутників (густина частот) hi можна знайти з таких міркувань: до першого інтервалу [1; 2,5] попадають дві варіанти — x1 = 1 і x2 = 2, частоти яких n1 = 5 і n2 = 1. Тому 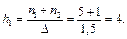 До другого інтервалу (2,5; 4] попадуть x3 = 3 і x4 = 4, частоти яких n3 = 8 і n4 = 3. Тому
До другого інтервалу (2,5; 4] попадуть x3 = 3 і x4 = 4, частоти яких n3 = 8 і n4 = 3. Тому 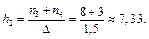 До інтервалу (4; 5,5] потрапила лише x5 = 5, частота якої n5 = 2. Тому
До інтервалу (4; 5,5] потрапила лише x5 = 5, частота якої n5 = 2. Тому 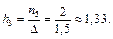 До четвертого інтервалу (5,5; 7] потраплять варіанти x6 = 6 і x7 = 7, частоти яких n6 = 2 і n7 = 6. Тому
До четвертого інтервалу (5,5; 7] потраплять варіанти x6 = 6 і x7 = 7, частоти яких n6 = 2 і n7 = 6. Тому 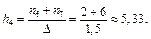
Отримаємо гістограму частот, зображену на рисунку 3.
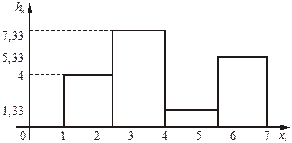
Рис. 3
Зазначимо, що сума площ прямокутників дорівнює об’єму вибірки
n = 5 + 1 + 8 + 3 + 2 + 2 + 6 = 27. ·
Дата добавления: 2015-08-26; просмотров: 1862;
