Інтервальні оцінки

Інтервальною називають оцінку, яка визначається числовим інтервалом. Довірчим називають інтервал (Q₁; Q₂), у який із заданою надійністю g (імовірністю, близькою до 1) потрапляє оцінюваний параметр Q:

P(Q₁ < Q < Q₂) = g, g ® 1.

Для повторної вибірки обсягом n середня вибіркова 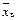є незміщеною і спроможною оцінкою середньої генеральної 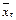. Якщо n доволі велике, тоді 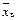з достатнім ступенем точності розподілена за нормальним законом із параметрами

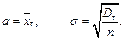
Для безповторної вибірки параметри відповідно рівні

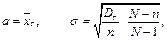
де N — обсяг генеральної сукупності.

Для повторної вибірки обсягом n середня вибіркова частка w є незміщеною і спроможною точковою оцінкою невідомої генеральної частки p. Якщо n доволі велике, тоді w з достатнім ступенем точності розподілена за нормальним законом із параметрами

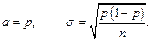
Для безповторної вибірки параметри відповідно рівні

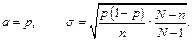
Проте N, як правило, доволі велике, тому приймають N – 1 = N.

Можливі значення, знайдені на основі даних простої вибірки, не співпадають із оцінюваними параметрами, і кожне таке неспівпадання називають помилкою репрезентативності, яка викликана тим, що досліджується не всі генеральна сукупність, а лише її частина. Тому виникає потреба в оцінці середніх величин таких помилок.

Середньою квадратичною помилкою при оцінювання середньої генеральної 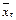та генеральної частки p називають середнє квадратичне відхилення середньої вибіркової 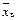та вибіркової частки w.

Можна вказати такі формули для визначення середніх квадратичних помилок:

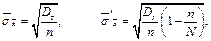
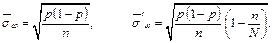
Тоді, щоб знайти довірчий інтервал 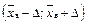з певною надійністю g, необхідно знайти граничну помилку D (найбільше відхилення середньої вибіркової або вибіркової частки від середньої генеральної чи генеральної частки відповідно, яке можливе для заданої довірчої ймовірності g) за формулою 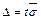, де t — корінь рівняння 2Ф(t) = g (див. додаток 2).

Формули для обчислення граничних помилок:

· для середньої вибіркової:

а) у випадку повторної вибірки: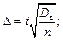

б) у випадку безповторної вибірки: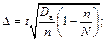

· для вибіркової частки:

а) у випадку повторної вибірки: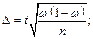

б) у випадку безповторної вибірки: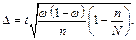

Приклад 6 У результаті статистичних досліджень випадкової величини X отримано вибірку обсягу n = 25 із таким статистичним розподілом:

Знайти з надійністю g = 0,99 інтервальну оцінку математичного сподівання а випадкової величини X за вибірковим середнім. Вважається, що випадкова величина X нормально розподілена.

Розв’язання. Оскільки в умові задачі не вказано, яка вибірка, то вважаємо, що вона є повторною. Перш ніж знайти довірчий інтервал для математичного сподівання 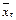= а випадкової величини X за формулою

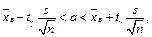
де 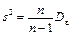— виправлена вибіркова дисперсія, необхідно визначити вибіркове середнє 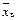, «виправлене» вибіркове середнє квадратичне відхилення s (n < 30) і t_g за додатком 2:

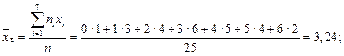
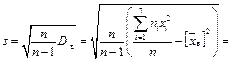
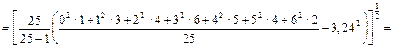
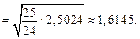
Тоді за додатком 2 знайдемо t з рівняння Ф(t) = 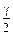, Ф(t) = 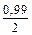, Ф(t) = 0,495, t = 2,58.

Шуканий довірчий інтервал

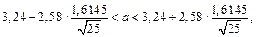
тобто

2,407 < a < 4,073. ·