Кореляційний і регресійний аналіз

Випадкові величини можуть бути незалежними або залежними. Вид залежності може бути функціональним, що трапляється рідко, або стохастичним, який полягає в тому, що при зміні можливих значень однієї випадкової величини відбувається зміна закону розподілу іншої. Найважливішим випадком такого зв’язку є кореляційний зв’язок.

Кореляційною залежністю називають залежність між значеннями однієї випадкової величини і умовним середнім значенням іншої. Вона має вигляд:

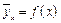
або

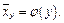
Перше рівняння називають рівнянням регресії Y на X, друге — рівнянням регресії X на Y, а їхні графіки — лініями регресії Y на X та X на Y. Якщо обидві лінії регресії — прямі, то кореляцію називають лінійною.

Вибірковим рівнянням прямої лінії регресії Y на X називають рівняння

,

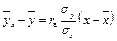де 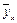— умовне середнє, 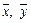— вибіркові середні випадкових величин X та Y відповідно, 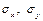— вибіркові середні квадратичні відхилення, r_в — вибірковий коефіцієнт кореляції, який дорівнює

,

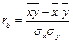де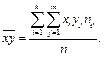

У випадку кореляції X на Y рівняння регресії має вигляд:

.

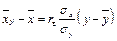Зазначимо, що r_в в обох рівняннях одне й теж. Воно характеризує тісноту лінійного зв’язку між випадковими величинами X та Y.

Дані рівняння одержані за допомогою методу найменших квадратів.

Кореляційна залежність може бути також і нелінійною, а саме, параболічною, гіперболічою, показниковою тощо. У цьому випадку рівняння регресії мають інший вигляд, функції f(x) і j(y) набувають відповідного вигляду. Так, наприклад, у випадку параболічної залежності

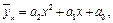
де a₀, a₁, a₂ — невідомі параметри. Щоб їх знайти, необхідно розв’язати систему нормальних рівнянь

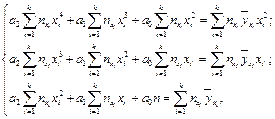
де 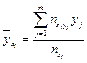— умовне середнє, m — кількість спостережуваних варіант випадкової величини Y, 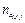— частота варіанти (x_i; y_j).

Приклад 7. Дано результати статистичних досліджень факторіальної ознаки x та результативної ознаки y:

Побудувати рівняння кореляційної залежності. Дані таблиці незгруповані.

Розв’язання. Для зручності згрупуємо дані, тобто запишемо до таблиці.

Y X						nx
	—			—	—
	—				—
		—		—	—
	—	—			—
	—	—	—	—	—
ny						n = 20

Визначимо характер зв’язку між X та Y.

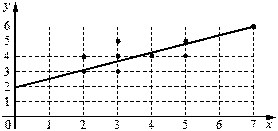
Рис. 4

Згідно графіка робимо висновок, що між x та y існує прямолінійна залежність, рівняння якої 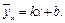Щоб знайти параметри k і b, запишемо канонічну систему рівнянь: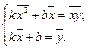

Проте рівняння прямолінійної регресії у вигляді 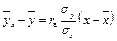зручніше, оскільки за величиною r_в можна зробити висновок про тісноту зв’язку між X та Y. Нагадаємо, що

,

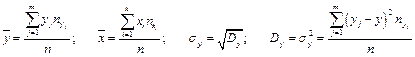або за розрахунковою формулою

Аналогічно для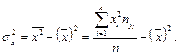

Наостанок, 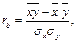де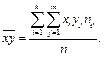

Отже,

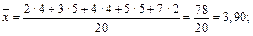
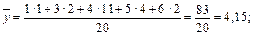
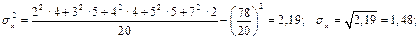
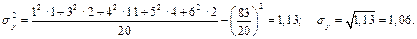
Обчислимо спочатку :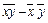

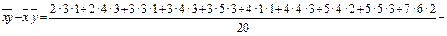
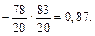
Тоді вибірковий коефіцієнт кореляції дорівнюватиме:

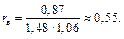
Таким чином, рівняння прямолінійної регресії має вигляд:

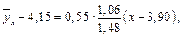
або

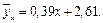
Отже, між величинами X та Y існує прямолінійна кореляція, рівняння регресії якої 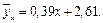При цьому вибірковий коефіцієнт кореляції 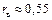свідчить про середній лінійний зв’язок між X та Y, до того ж, оскільки 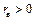, то має місце додатна кореляція, тобто при зростанні X зростає відповідне значення результативної ознаки Y.