Числові характеристики вибірки
Середнє арифметичне значення вибірки називають вибірковим середнім 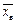 і обчислюють за формулами
і обчислюють за формулами
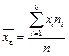 або
або 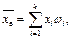
де xі — значення i-ї варіанти; ni — частота i-ї варіанти; n — обсяг вибірки; k — кількість варіант у вибірці; wi — відносна частота i-ї варіанти.
Середнє значення квадрата відхилення значень елементів вибірки від вибіркового середнього називають вибірковою дисперсією Dв і обчислюють за формулами
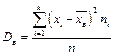 або
або 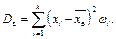
Після перетворень формули для знаходження вибіркової дисперсії дещо спрощуються:
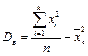 або
або 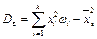 .
.
тобто вибіркова дисперсія дорівнює різниці середнього квадрата елементів вибірки й квадрата вибіркового середнього.
Квадратний корінь з вибіркової дисперсії 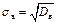 називають середнім квадратичним відхиленням вибірки.
називають середнім квадратичним відхиленням вибірки.
Приклад 4. Задано статистичний розподіл вибірки:
| хi | |||||||
| ni |
Знайти вибіркове середнє, вибіркову дисперсію та середнє квадратичне відхилення вибірки.
Розв’язання. Обчислимо обсяг вибірки:
n = 5 + 2 + 12 + 7 + 4 + 3 + 2 = 35.
Знайдемо відповідно вибіркове середнє, вибіркову дисперсію та середнє квадратичне відхилення вибірки:
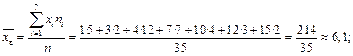
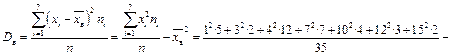
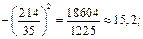
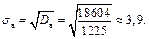 ·
·
Медіаною (Ме) називають значення середнього елемента варіаційного ряду. Якщо обсяг вибірки n = 2m + 1 непарний, то медіаною буде значення елемента варіаційного ряду з номером m + 1:
Ме = хm+1.
Якщо обсяг вибірки n = 2m парний, то медіаною буде середнє значення елементів варіаційного ряду з номерами m і m + 1:
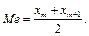
Якщо задано інтервальний статистичний розподіл вибірки, то спочатку знаходять медіанний частинний інтервал, тобто перший частинний інтервал, для якого сума частот усіх попередніх частинних інтервалів з даним включно перевищує половину обсягу вибірки. У цьому разі медіану знаходять за формулою
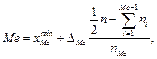
де 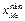 — початок медіанного частинного інтервалу;
— початок медіанного частинного інтервалу; 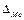 — довжина медіанного частинного інтервалу; n — обсяг вибірки;
— довжина медіанного частинного інтервалу; n — обсяг вибірки; 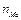 — частота медіанного частинного інтервалу; Ме –1 — номер попереднього до медіанного частинного інтервалу.
— частота медіанного частинного інтервалу; Ме –1 — номер попереднього до медіанного частинного інтервалу.
Приклад 5. На одному з відрізків залізниці планується створити зупинку пасажирського поїзда. Розподіл населених пунктів з чисельністю їх населення наведено в таблиці.
| На якому кілометрі залізниці розташований населений пункт, км | |||||||
| Чисельність населення, тис. оcіб |
На якому кілометрі залізниці потрібно розташувати цю зупинку, щоб сумарна відстань, яку покриватимуть потенційні пасажири до цієї зупинки, була найменшою.
Розв’язання. Оскільки медіана має властивість, що сума абсолютних величин відхилень елементів вибірки від медіани менша, ніж від будь-якої іншої величини, то для розв’язання прикладу потрібно знайти медіану.
Спочатку визначимо обсяг вибірки:
n = 5 + 2 + 3 + 10 + 1 + 4 + 6 = 31.
Отже, серединою (середнім членом) варіаційного ряду буде елемент із номером 16: Ме = х16. Оскільки варіаційний ряд можна записати у вигляді
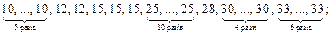
легко бачити, що х16 = 25, тобто зупинку слід розташувати на 25-му кілометрі залізниці. ·
Модою (Мо) називають варіанту з найбільшою частотою. У випадку інтервального статистичного розподілу вибірки з однаковими за довжиною частинними інтервалами модальний частинний інтервал визначається за найбільшою частотою, а при різних за довжиною частинних інтервалах — за найбільшою густиною 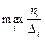 , де ni, Di — відповідно частота та довжина і-го частинного інтервалу. У цьому разі моду знаходять за формулою
, де ni, Di — відповідно частота та довжина і-го частинного інтервалу. У цьому разі моду знаходять за формулою
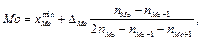
де 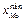 — початок модального частинного інтервалу;
— початок модального частинного інтервалу; 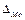 — довжина модального частинного інтервалу;
— довжина модального частинного інтервалу; 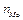 — частота модального частинного інтервалу;
— частота модального частинного інтервалу; 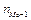 — частота попереднього до модального частинного інтервалу;
— частота попереднього до модального частинного інтервалу; 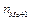 — частота наступного за модальним частинного інтервалу.
— частота наступного за модальним частинного інтервалу.
Варіаційним розмахом називають різницю між найбільшим і найменшим значеннями вибірки:
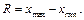
Дата добавления: 2015-08-26; просмотров: 3000;
