Точкові оцінки
Статистичною оцінкою Q* невідомого параметра Q теоретичного розподілу називають функцію f(Х1, Х2, ..., Хn) від спостережуваних випадкових величин Х1, Х2, ..., Хn.
Точковою називають статистичну оцінку, яка визначається одним єдиним числом Q* = f(x1, x2, ..., xn), де x1, x2, ..., xn — результати n спостережень над кількісною ознакою випадкової величини X (вибірка).
Незміщеною називають точкову оцінку Q*, математичне сподівання якої дорівнює оцінюваному параметру Q за будь-якого обсягу вибірки:
М(Q*) = Q.
Зміщеною називають точкову оцінку Q*, математичне сподівання якої відмінне від оцінюваного параметра Q:
М(Q*) ¹ Q.
Незміщеною оцінкою генерального середнього (математичного сподівання) є вибіркове середнє
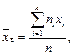
де nі — частота варіанти хi; xі — варіанта вибірки; 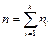 — обсяг вибірки.
— обсяг вибірки.
Зміщеною оцінкою генеральної дисперсії є вибіркова дисперсія
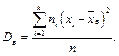
Ця оцінка зміщена, оскільки
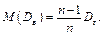
Незміщеною оцінкою генеральної дисперсії є виправлена вибіркова дисперсія
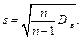
Для обчислення вибіркової дисперсії можна скористатися більш зручною формулою
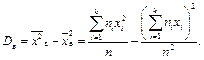
Дата добавления: 2015-08-26; просмотров: 894;
