Неперервні випадкові величини
Неперервною випадковою величиною називають величину, функція розподілу якої є неперервною.
Найпростішим і найпоширенішим способом задання розподілу неперервної випадкової величини є задання її функції розподілу F(x). Крім того, можна задати випадкову величину і через густину розподілу випадкової величини (диференціальною функцією розподілу) f(x):
f(x) = F¢ (x).
Очевидно, що:
1) f(x) ³ 0;
2) 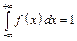 ;
;
3) 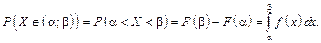
Якщо відома диференціальна функція, то формула для обчислення інтегральної функції F(x) має вигляд:
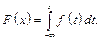
Найважливішими є такі типи неперервних розподілів: рівномірний, нормальний та експоненціальний.
Розподіл випадкової величини називають рівномірним на [a; b], якщо диференціальна функція має вигляд:
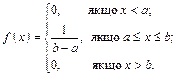
Функція розподілу має вигляд:
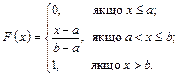
Розподіл випадкової величини називають експоненціальним (показниковим) з параметром l > 0, якщо його диференціальна функція має вигляд:
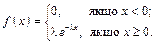
Функція розподілу має вигляд:
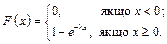
Розподіл випадкової величини називають нормальним з параметрами a та s, якщо його густина розподілу має вигляд:
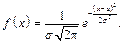
Функція y = f(x) швидко спадає, якщо x ® ±¥. Площа фігури, обмеженої графіком функції y = f(x) і віссю Ох, дорівнює 1.
Імовірність того, що нормально розподілена величина набуде значення, яке належить відрізку [a; b], обчислюється так:
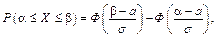
де Ф(х) — інтегральна функція Лапласа.
Зазначимо, що ймовірностний зміст параметрів a та s полягає втому, що
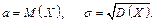
Імовірність того, що відхилення нормально розподіленої величини від свого математичного сподівання за абсолютною величиною не перевищить деяке число e ³ 0, обчислюють так:
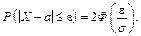
Приклад 15. Випадкова величина X розподілена за нормальним законом, математичне сподівання якого a = 4. Знайти ймовірність того, що випадкова величина відхилиться від свого математичного сподівання на величину, що не перевищує потроєного середнього квадратичного відхилення.
Розв’язання.
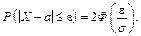
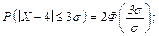
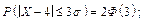
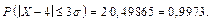 ·
·
Даний приклад дає можливість сформулювати правило «трьох s»: нормально розподілена випадкова величина набуває своїх значень з інтервалу
[a – 3s; a + 3s], якщо ж ця випадкова величина набуває значень за межами даного інтервалу, то вони є малоймовірними.
Математичним сподіванням неперервної випадкової величини називають число
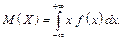
Дисперсію неперервної випадкової величини обчислюють як
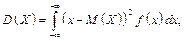
або за другою розрахунковою формулою,
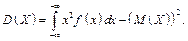
Приклад 16. Випадкову величину X задано густиною розподілу:
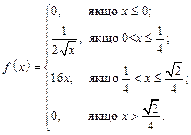
Знайти числові характеристики даної випадкової величини.
Розв’язання. Математичне сподівання випадкової величини Х обчислимо за формулою 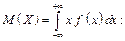
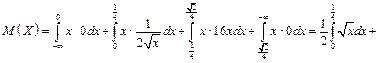
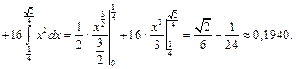
За формулою 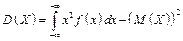 знайдемо дисперсію випадкової величини Х:
знайдемо дисперсію випадкової величини Х:
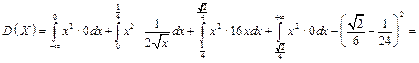
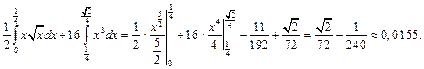
Середнє квадратичне відхилення випадкової величини X
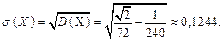 ·
·
Дата добавления: 2015-08-26; просмотров: 1379;
